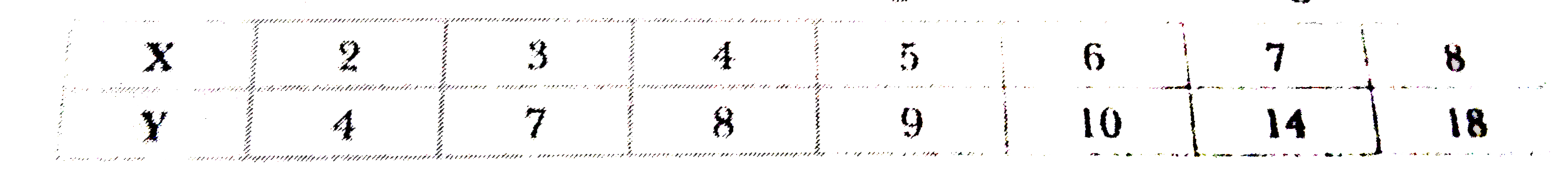Coefficient of coupling is given by:
k=ML1L2
k=M√L1L2
k=L1L2√M
Both (a) and (c)
To solve the question regarding the coefficient of coupling, we can break it down step by step.
1. Understanding Coefficient of Coupling:
The coefficient of coupling (denoted as k) is a measure of how effectively magnetic flux is transferred from one coil (the primary) to another coil (the secondary). It ranges from 0 to 1, where 0 indicates no coupling and 1 indicates perfect coupling.
2. Mathematical Definition:
The coefficient of coupling can be mathematically defined as:
k=m√L1L2
where:
- m is the mutual inductance between the coils,
- L1 is the self-inductance of the primary coil,
- L2 is the self-inductance of the secondary coil.
3. Rearranging the Formula:
From the above equation, we can express m in terms of k, L1, and L2:
m=k⋅√L1L2
4. Understanding the Range of k:
The coefficient of coupling k must satisfy the condition:
0≤k≤1
This indicates that the maximum value of k is 1, which corresponds to the scenario where all the magnetic flux from the primary coil links perfectly with the secondary coil.
5. Conclusion:
Therefore, the coefficient of coupling is a crucial parameter in understanding the efficiency of energy transfer between two inductively coupled coils.
Final Answer:
The coefficient of coupling is given by:
k=m√L1L2
The coefficient of coupling (denoted as k) is a measure of how effectively magnetic flux is transferred from one coil (the primary) to another coil (the secondary). It ranges from 0 to 1, where 0 indicates no coupling and 1 indicates perfect coupling.
The coefficient of coupling can be mathematically defined as:
k=m√L1L2
where:
- m is the mutual inductance between the coils,
- L1 is the self-inductance of the primary coil,
- L2 is the self-inductance of the secondary coil.
From the above equation, we can express m in terms of k, L1, and L2:
m=k⋅√L1L2
The coefficient of coupling k must satisfy the condition:
0≤k≤1
This indicates that the maximum value of k is 1, which corresponds to the scenario where all the magnetic flux from the primary coil links perfectly with the secondary coil.
Therefore, the coefficient of coupling is a crucial parameter in understanding the efficiency of energy transfer between two inductively coupled coils.
The coefficient of coupling is given by:
k=m√L1L2
Topper's Solved these Questions
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER SELF- ASSESSMENT -(10)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF- ASSESSMENT -(10)EXERCISE - SECTION-B
17 Videos
Similar Questions
Knowledge Check
Coefficient of coupling between two coils of self-inductances L1 and L2 is unity. It means
A50% flux of L1 is linked with L2B100% flux of L1 is linked with L2C√L1 time of flux of L1 is linked with L2DNone of the aboveTwo identical solenoid coils, each of self inductancen L are connected in series. Their turns are in the same sense, and the distance between them is such that the coefficient of coupling is half . Then the equivalent inductance of the combination is ___
ALB2LC3LDL/2The coefficient of coupling between two coil is maximum when the two coils are ___
Aplaced at right anglesBplaced parallel at close distanceCwound around a commen ferromagnetic core and insulated from itDplaced at an angle of 45∘ with each other
Calculate coefficient of variation, given the following data-set:
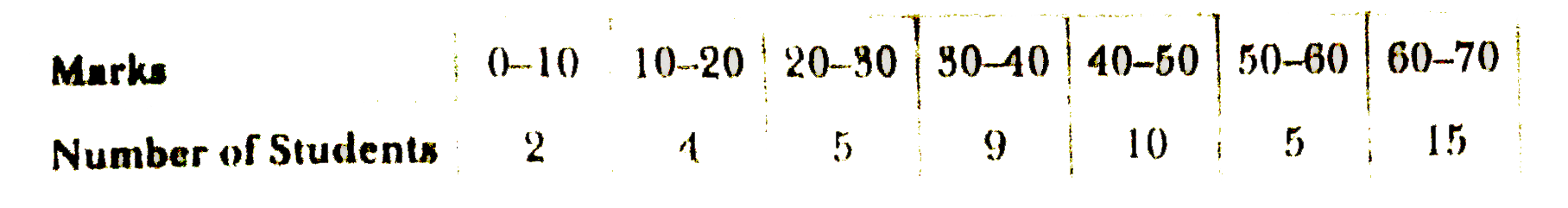
View Solution
Find the coefficient of variation for the given distribution .
View SolutionCoupling and repulsion theory of linkage was given by
View SolutionMoment of couple is called
View SolutionJoule Thomson coefficient is given by the expression
View Solution