Find the new capacitance if two dielectric of dielectric constant 4 and 6 are filled in a capacitor of capacitance
Step by step video & image solution for Find the new capacitance if two dielectric of dielectric constant 4 and 6 are filled in a capacitor of capacitance 1muF by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER SELF- ASSESSMENT -(10)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF- ASSESSMENT -(10)EXERCISE - SECTION-B
17 Videos
Similar Questions
If half the space between two concentric conducting spheres be filled with dielectric of dielectric constant k and the rest is filled with air. Show that the capacitance of the capacitor thus formed will be same as if the whole part is filled with the dielectric of dielectric constant 12(1+k):
View SolutionDefine the term 'dielectric constant of a medium in terms of capacitance.
View Solution
Knowledge Check
Assertion (A): If the distance between plates of a parallel plate capacitor is halved and the intervening space is filled with a dielectric of dielectric constant 3, the capacitance of capacitor becomes 6 times of its original capacitance.
Reason (R) : The capacitance of a capacitor does not depend on the material of the metal plates.AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion is false but reason is true.A parallel plate capacitor 'A' of capacitance 1μF is charged to a potential drop 100 volt and then disconnected form the battery. Now the capacitor 'A' is completely filled with a dielectric slap of dielectric constant k=4. Another parallel plate capacitor 'B' of capacitance 2μF is charged to a potential drop 20 volt and then disconnected from the battery. Now the two capacitors 'A' and 'B' are connected with each other with opposite polarities. Then the heat dissipated after connecting the capacitors is
A1.15×10−3JB1.25×10−3JC1.35×10−3JD1.45×10−13JA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA capacitor is filled with two dielectrics of same dimensions, but of dielectric constants 2 and 3 respectively. Find the ratio of capacitances in the two arrangements shown in Fig.

View SolutionA parallel plate air capacitor has a capacitance C. The capacitor is half-filled with a dielectric of dielectric constant 5. The percentage increase in the capacitance must have been -- %.
View SolutionA parallel plate capacitor has a capacitance of 6μF. If the separation between the plates is reduced to one half of its original separation and a dielectric of dielectric constant 3 is introduced between the plates of capacitor, its new capacitance will be __________ .
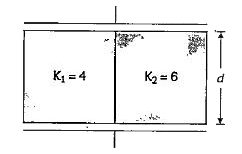
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View Solution
