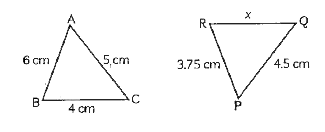
AD and PM are medians of triangles ABC and PQR respectively where ΔABC~ΔPQR. Prove that: ABPQ=ADPM.
Step by step video & image solution for AD and PM are medians of triangles ABC and PQR respectively where Delta ABC ~ Delta PQR. Prove that: (AB)/(PQ)=(AD)/(PM). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 03 (MATHEMATICS)Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 03 (MATHEMATICS)Exercise:SECTION D
Explore 12 Videos
- SAMPLE PAPER 03 (MATHEMATICS)Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 03 (MATHEMATICS)Exercise:SECTION B
Explore 9 Videos
- SAMPLE PAPER 03Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 03Exercise:Section - C
Explore 10 Videos
- SAMPLE PAPER 07Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 07Exercise:SECTION -C
Explore 10 Videos
Similar Questions
Knowledge Check
If PS is median of the triangle PQR, then ar(ΔPQS): ar(ΔQRP) is
 A1 : 1B2 : 1C1 : 2DCan't be determined
A1 : 1B2 : 1C1 : 2DCan't be determined
If AD, BE and CF are medians of triangle ABC then prove that median AD divides line segment EF.
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
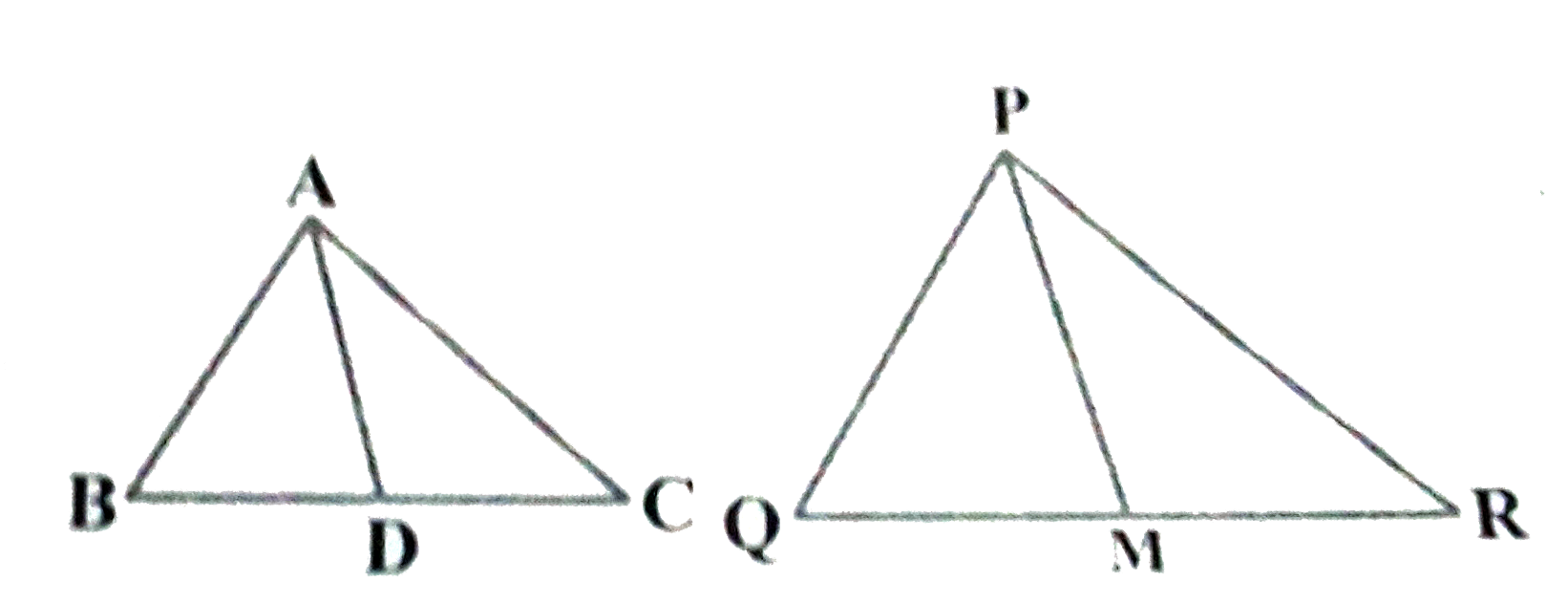
View SolutionSides AB and BC and median AD of a triangle ABC are respectively propor-/ tional to sides PQ and QR and median PM of ΔPQR (see Fig. 6.41). Show that ΔABC~ΔPOR.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
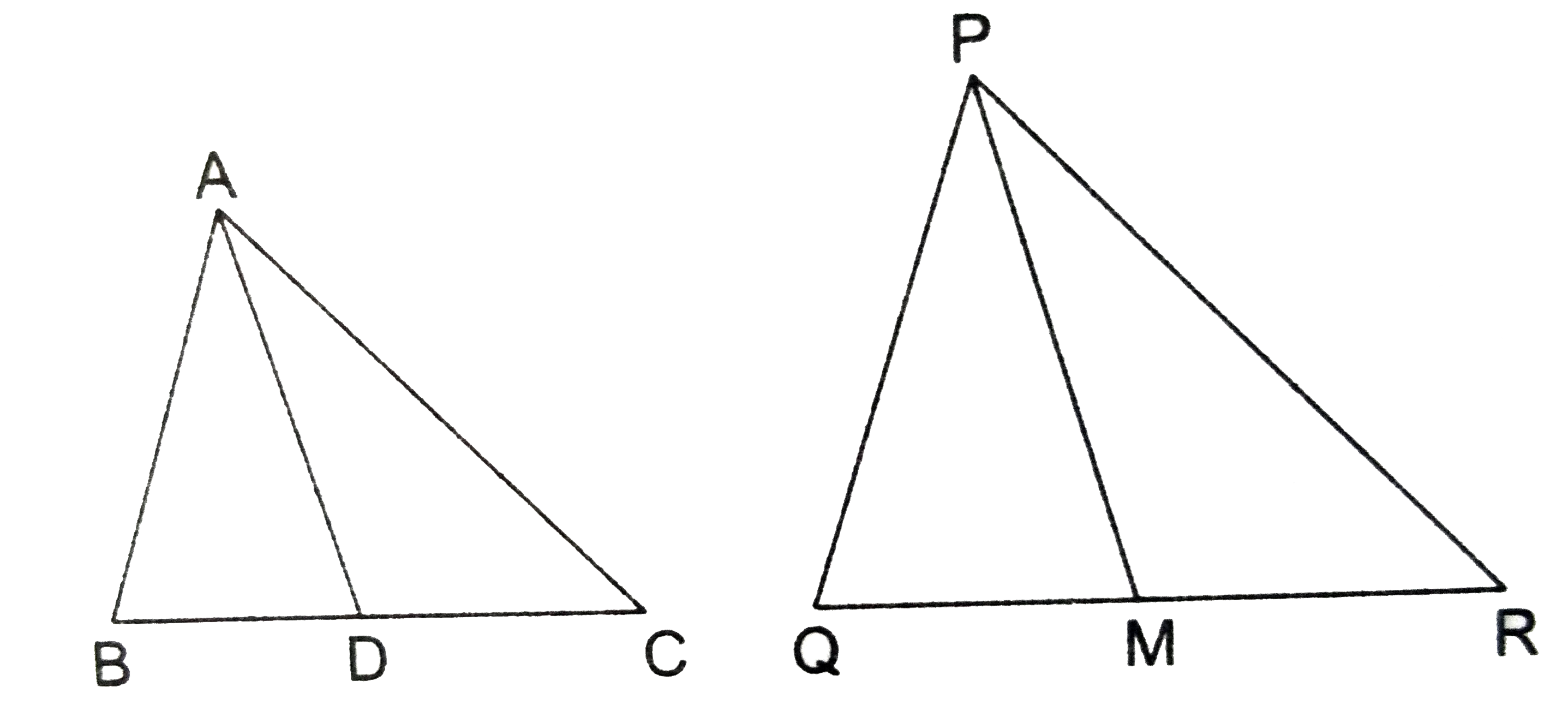
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionIn △ ABC, AD is a median. Prove that AB + AC > 2AD
View Solution