StateP1,V1,T1ARev−−→State BP2,V2,T2: If P1=P2 then
ΔSuniverse=0
ΔSuniverse=1
ΔSuniverse>0
ΔSuniverse<0
To solve the problem, we need to analyze the conditions given for the transition from state A to state B under the constraints of pressure being constant (isobaric process) and the fact that the pressures in both states are equal (P1 = P2).
1. Identify the Process Type:
Since we are given that P1 = P2, we can conclude that the process from state A to state B is isobaric (constant pressure).
Hint: Remember that an isobaric process is characterized by constant pressure throughout the transition.
2. Understand the Implications of Isobaric Process:
In an isobaric process, the volume and temperature can change, but the pressure remains constant. This means that as the system transitions from state A to state B, the temperature (T1 to T2) and volume (V1 to V2) may vary.
Hint: In an isobaric process, the equation governing the change in entropy (ΔS) is given by ΔS = Cp * ln(T2/T1), where Cp is the molar heat capacity at constant pressure.
3. Apply the Entropy Change Formula:
For an isobaric process, the change in entropy (ΔS) can be calculated using the formula:
ΔS=Cp⋅ln(T2T1)
Here, Cp is the molar heat capacity at constant pressure.
Hint: The change in entropy depends on the ratio of the final and initial temperatures.
4. Consider the Case of Reversible Process:
The problem states that the process is reversible. In a reversible isobaric process, the entropy change can be zero if the temperatures are equal (T1 = T2). However, if T1 and T2 are different, ΔS will not be zero.
Hint: For a reversible process, if the initial and final temperatures are the same, the change in entropy will be zero.
5. Conclusion:
If P1 = P2 and the process is isobaric and reversible, the change in entropy (ΔS) will depend on the ratio of temperatures. If T1 = T2, then ΔS = 0. Otherwise, ΔS will be positive or negative depending on whether T2 is greater than or less than T1.
Final Answer: If P1 = P2, then ΔS = C_p * ln(T2/T1). If T1 = T2, then ΔS = 0.
Since we are given that P1 = P2, we can conclude that the process from state A to state B is isobaric (constant pressure).
In an isobaric process, the volume and temperature can change, but the pressure remains constant. This means that as the system transitions from state A to state B, the temperature (T1 to T2) and volume (V1 to V2) may vary.
For an isobaric process, the change in entropy (ΔS) can be calculated using the formula:
ΔS=Cp⋅ln(T2T1)
Here, Cp is the molar heat capacity at constant pressure.
The problem states that the process is reversible. In a reversible isobaric process, the entropy change can be zero if the temperatures are equal (T1 = T2). However, if T1 and T2 are different, ΔS will not be zero.
If P1 = P2 and the process is isobaric and reversible, the change in entropy (ΔS) will depend on the ratio of temperatures. If T1 = T2, then ΔS = 0. Otherwise, ΔS will be positive or negative depending on whether T2 is greater than or less than T1.
Similar Questions
A system X undergoes following changes
XP1V1T1→WP2V2T1→ZP3V2T2→XP1V1T1
The overall process may be called as
View SolutionOne mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View SolutionA gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
View SolutionPt∣∣∣H2(p1)∣∣∣H+(1M)∣∣∣∣∣∣H+(1M)∣∣∣H2(p2)∣∣∣Pt (where p1 and p2 are pressure) cell reaction cell reaction will be spontaneous if:
View SolutionFor an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
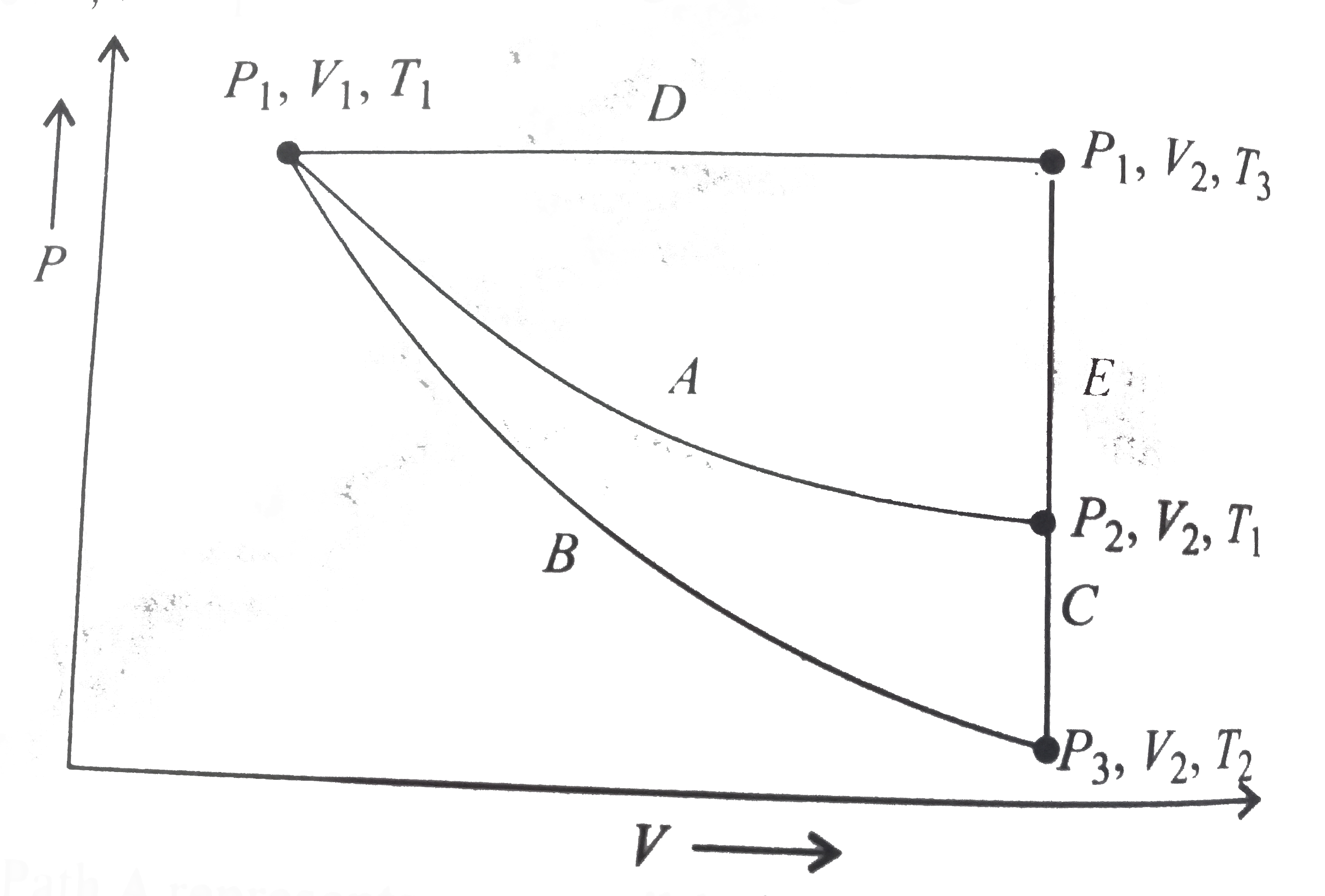
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
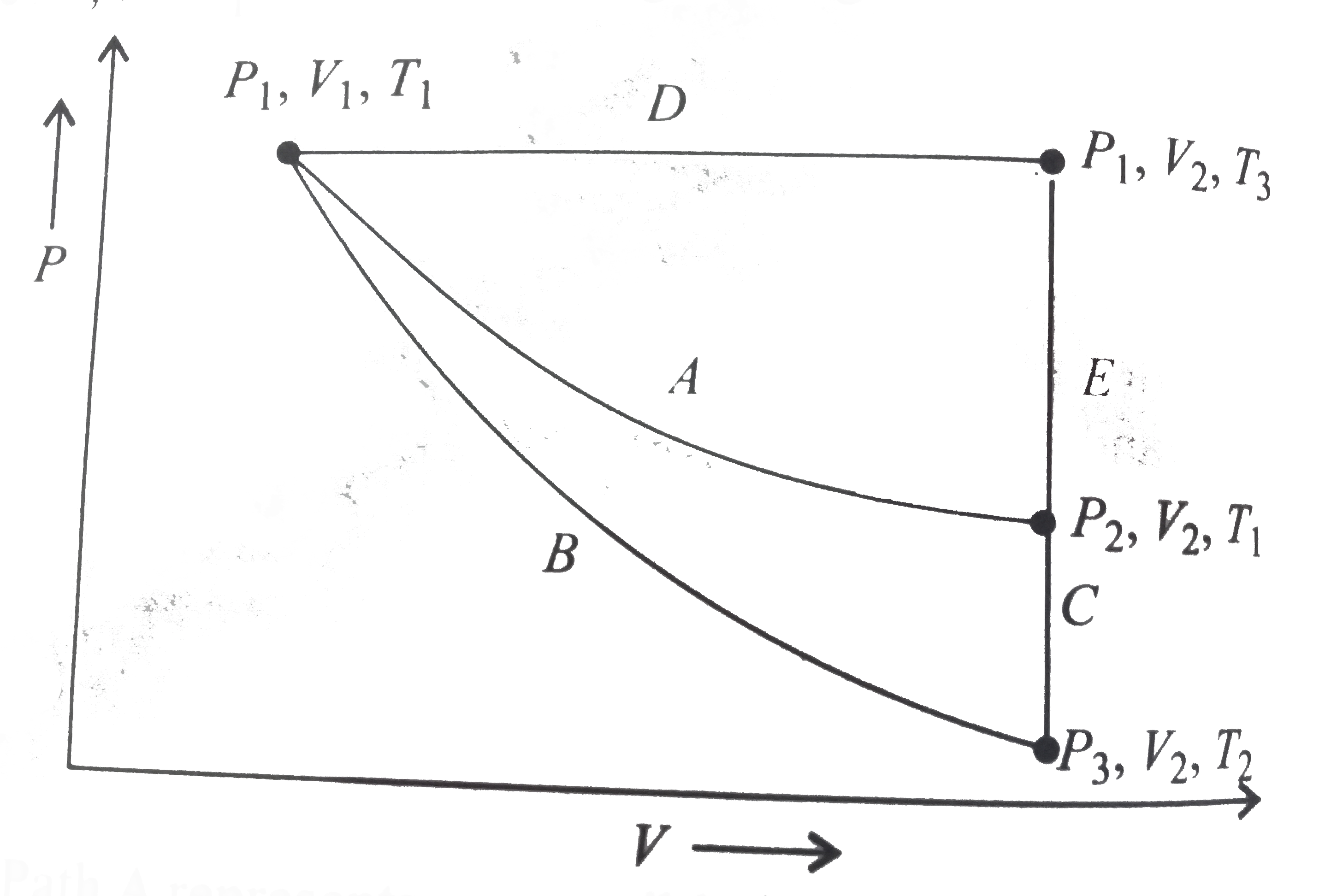
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
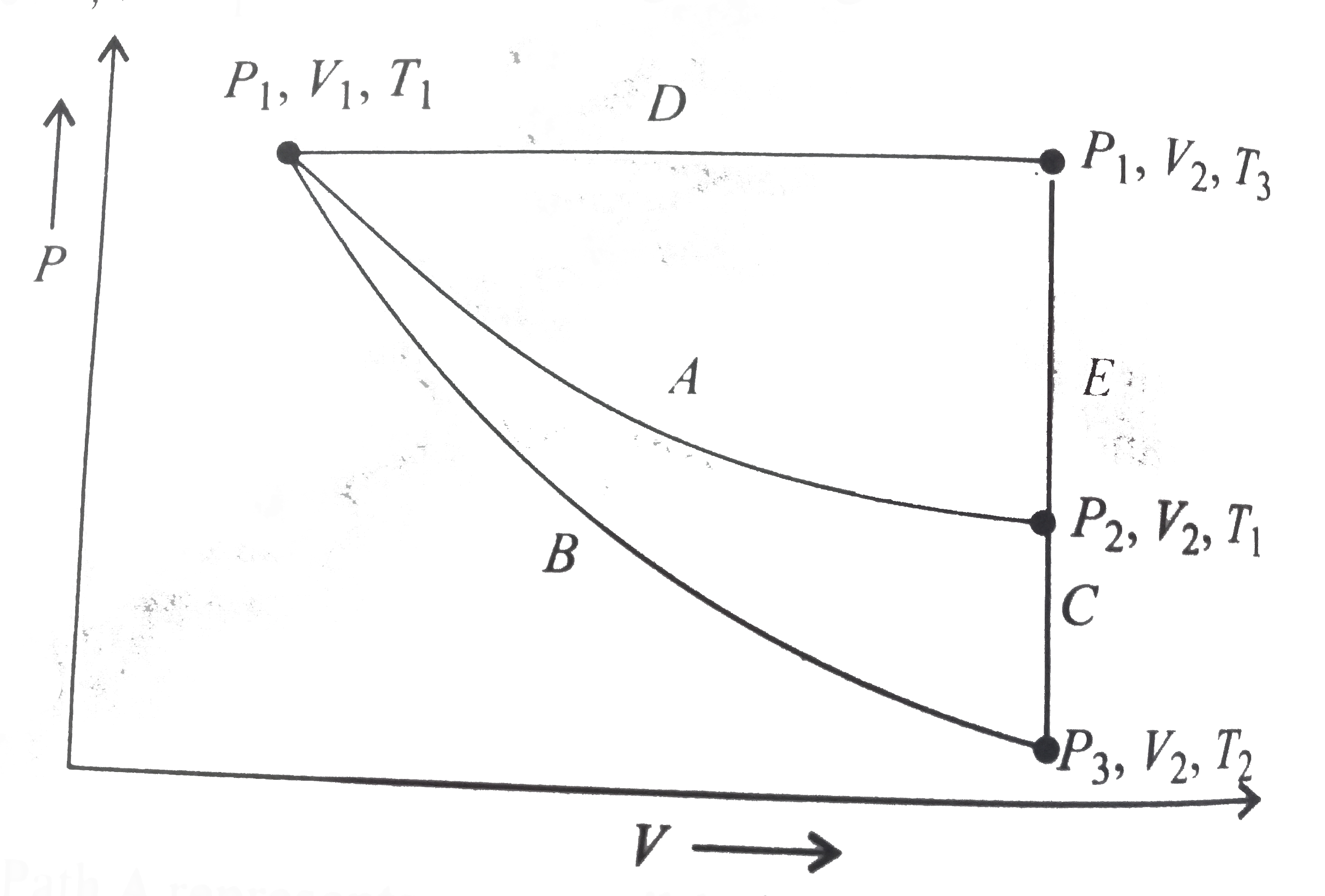
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View SolutionExamine the following plots and predict whether in (i) P1<P2andT1>T2 , in (ii) T1=T2<T3, in (iii) V1>V2,in(iv)P1>P2orP2>P1
_E01_267_Q01.png)
View Solution
