A gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
nR(T1−T2)γ−1
p1V1−p2V2γ−1
p1V1−p2V2γ+1
nRT(T1−T2)
The correct Answer is:A, B
To find the work done by the gas during an adiabatic process, we can follow these steps:
Step 1: Understand the Adiabatic Process
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between pressure (P), volume (V), and temperature (T) for an ideal gas can be described using the adiabatic condition:
PVγ=constant
where γ=CpCv.
Step 2: Express Work Done in Terms of Volume
The work done W by the gas during an adiabatic process can be expressed as:
W=∫V2V1PdV
Step 3: Substitute Pressure Using the Adiabatic Condition
From the adiabatic condition, we have:
P=KVγ
where K is a constant. Therefore, we can rewrite the work done as:
W=∫V2V1KVγdV
Step 4: Perform the Integration
Now we can perform the integration:
W=K∫V2V1V−γdV
The integral of V−γ is:
∫V−γdV=V1−γ1−γ
Thus, we have:
W=K(V1−γ1−γ)V2V1
W=K1−γ(V1−γ2−V1−γ1)
Step 5: Relate K to Pressure and Volume
Since K is constant, we can express it in terms of the initial and final states:
K=P1Vγ1=P2Vγ2
Substituting this into the work equation gives:
W=P2Vγ21−γ(V1−γ2−V1−γ1)
Step 6: Simplify the Expression
Using the relationship P1Vγ1=P2Vγ2, we can further simplify:
W=11−γ(P2V2−P1V1)
Step 7: Relate Work Done to Temperature
Using the ideal gas law PV=nRT, we can express the work done in terms of temperatures:
W=nR1−γ(T2−T1)
Final Result
Thus, the work done by the gas during the adiabatic process is:
W=nR(T2−T1)1−γ
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between pressure (P), volume (V), and temperature (T) for an ideal gas can be described using the adiabatic condition:
PVγ=constant
where γ=CpCv.
The work done W by the gas during an adiabatic process can be expressed as:
W=∫V2V1PdV
From the adiabatic condition, we have:
P=KVγ
where K is a constant. Therefore, we can rewrite the work done as:
W=∫V2V1KVγdV
Now we can perform the integration:
W=K∫V2V1V−γdV
The integral of V−γ is:
∫V−γdV=V1−γ1−γ
Thus, we have:
W=K(V1−γ1−γ)V2V1
W=K1−γ(V1−γ2−V1−γ1)
Since K is constant, we can express it in terms of the initial and final states:
K=P1Vγ1=P2Vγ2
Substituting this into the work equation gives:
W=P2Vγ21−γ(V1−γ2−V1−γ1)
Using the relationship P1Vγ1=P2Vγ2, we can further simplify:
W=11−γ(P2V2−P1V1)
Using the ideal gas law PV=nRT, we can express the work done in terms of temperatures:
W=nR1−γ(T2−T1)
Thus, the work done by the gas during the adiabatic process is:
W=nR(T2−T1)1−γ
Similar Questions
One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
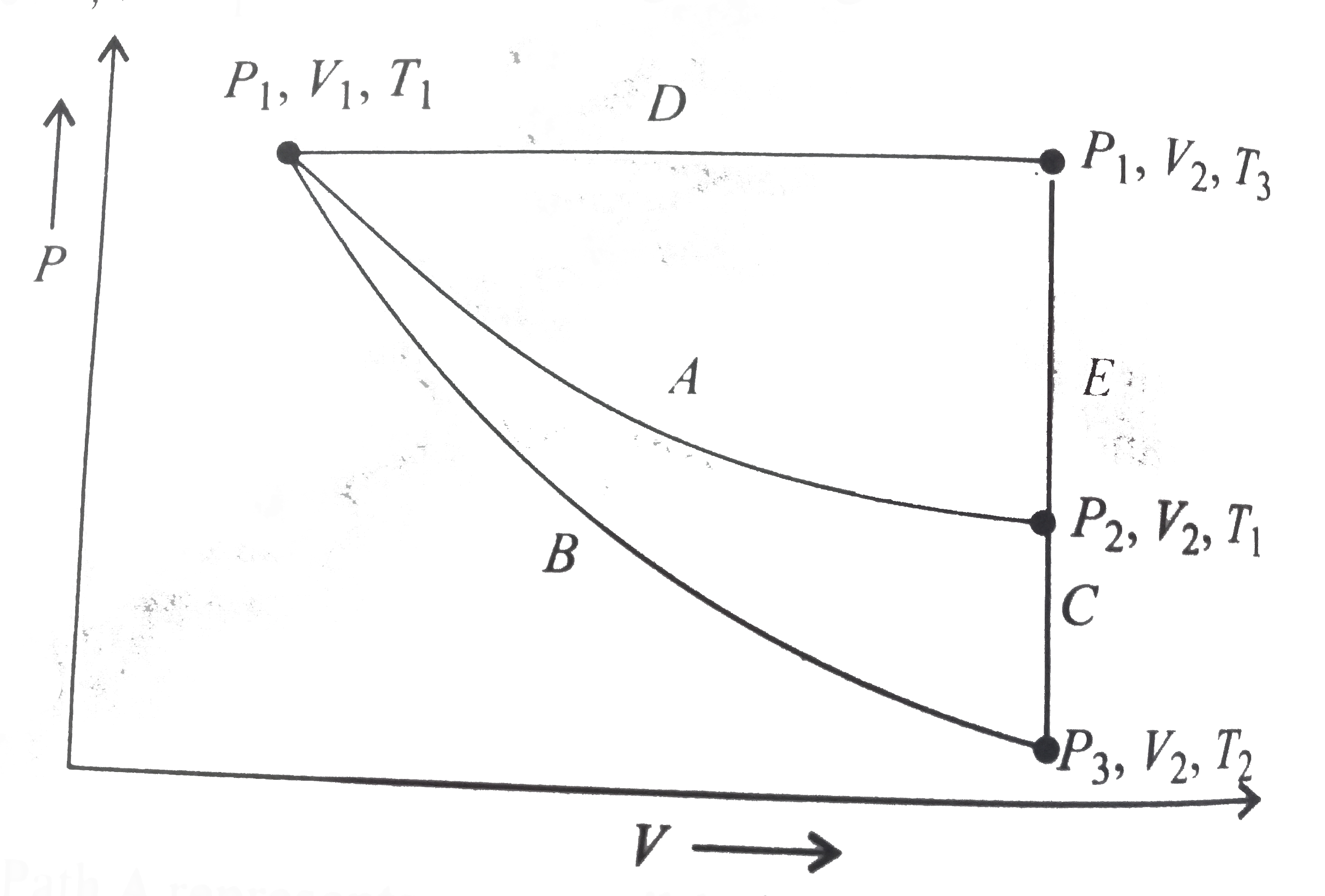
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
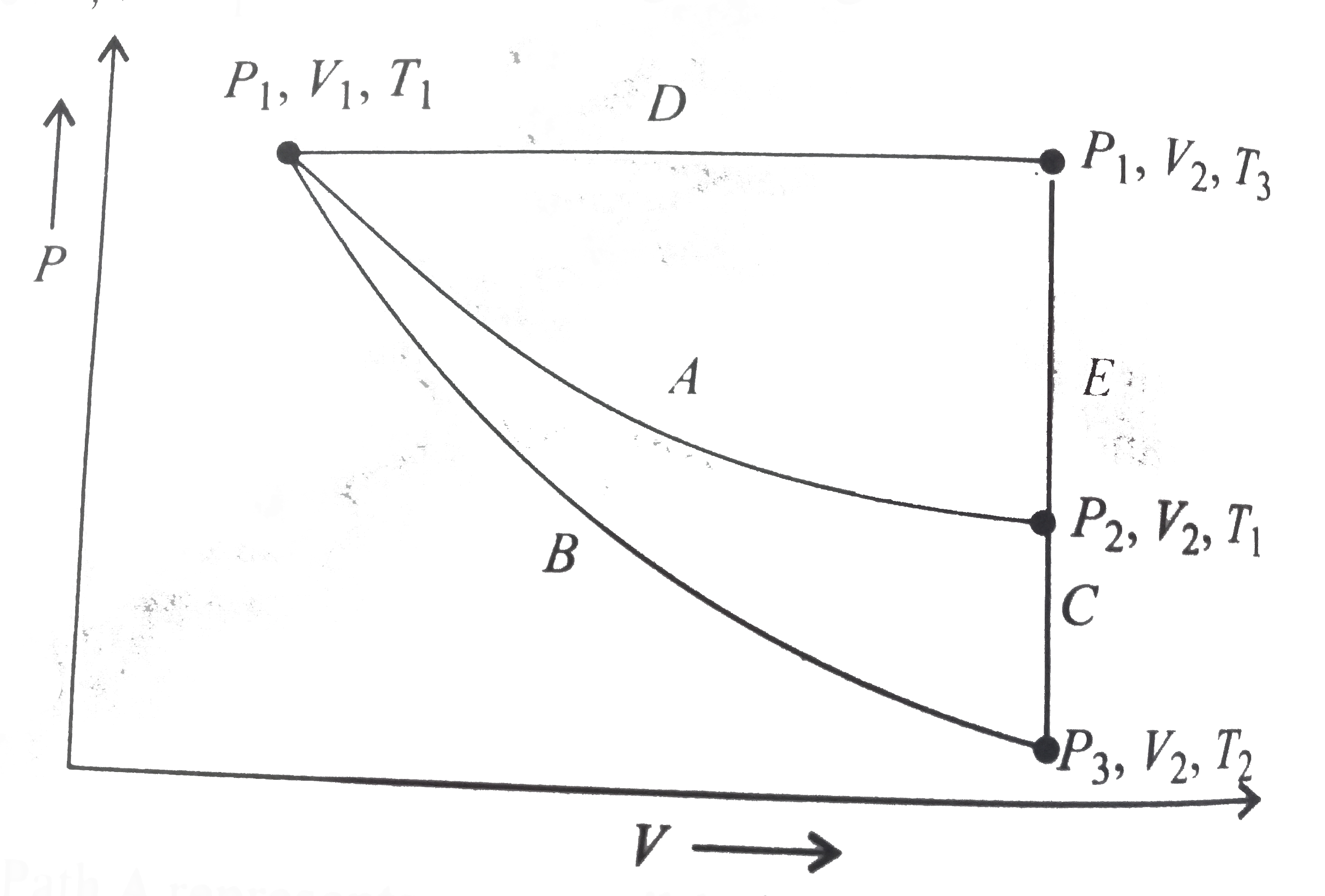
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
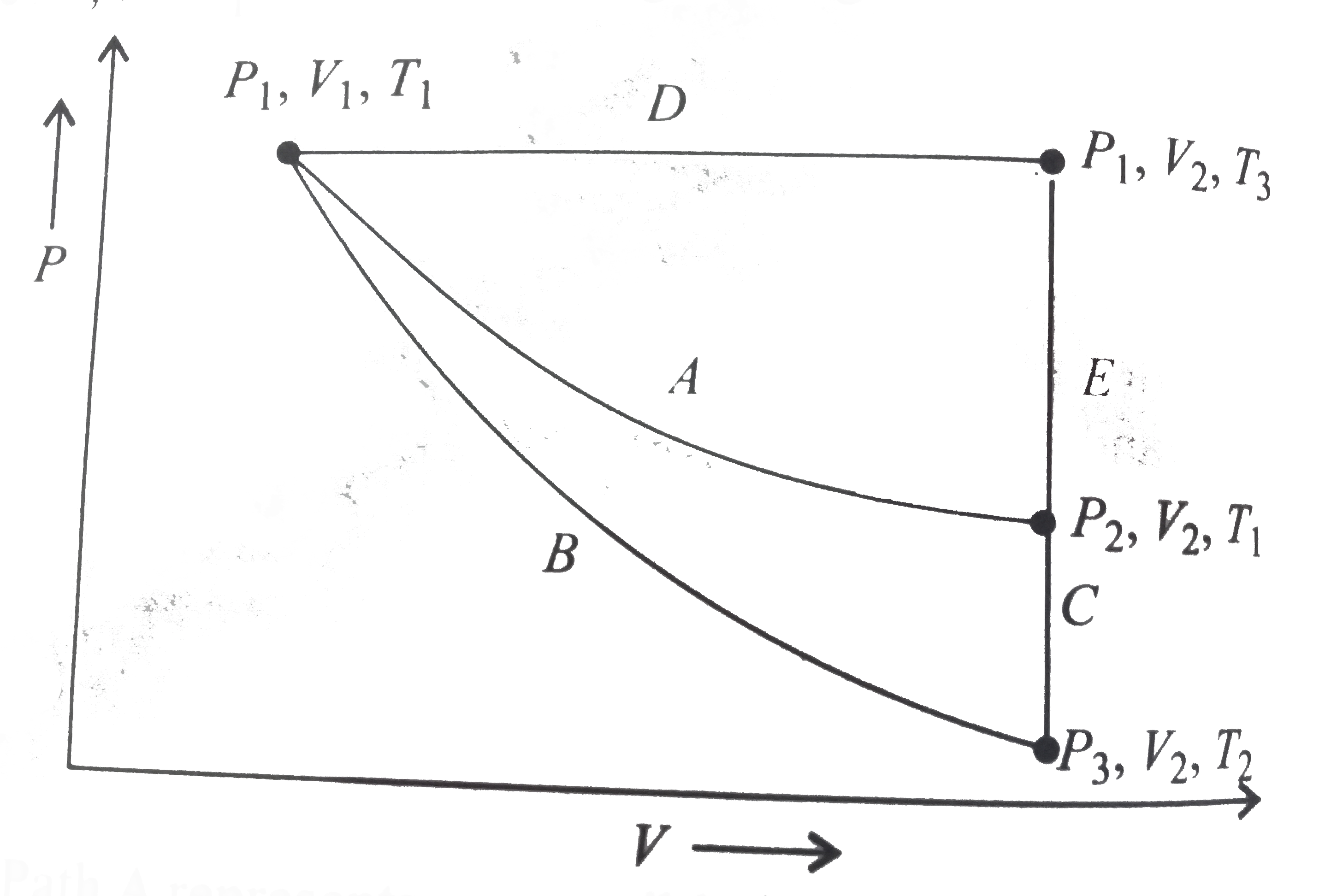
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionAn ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
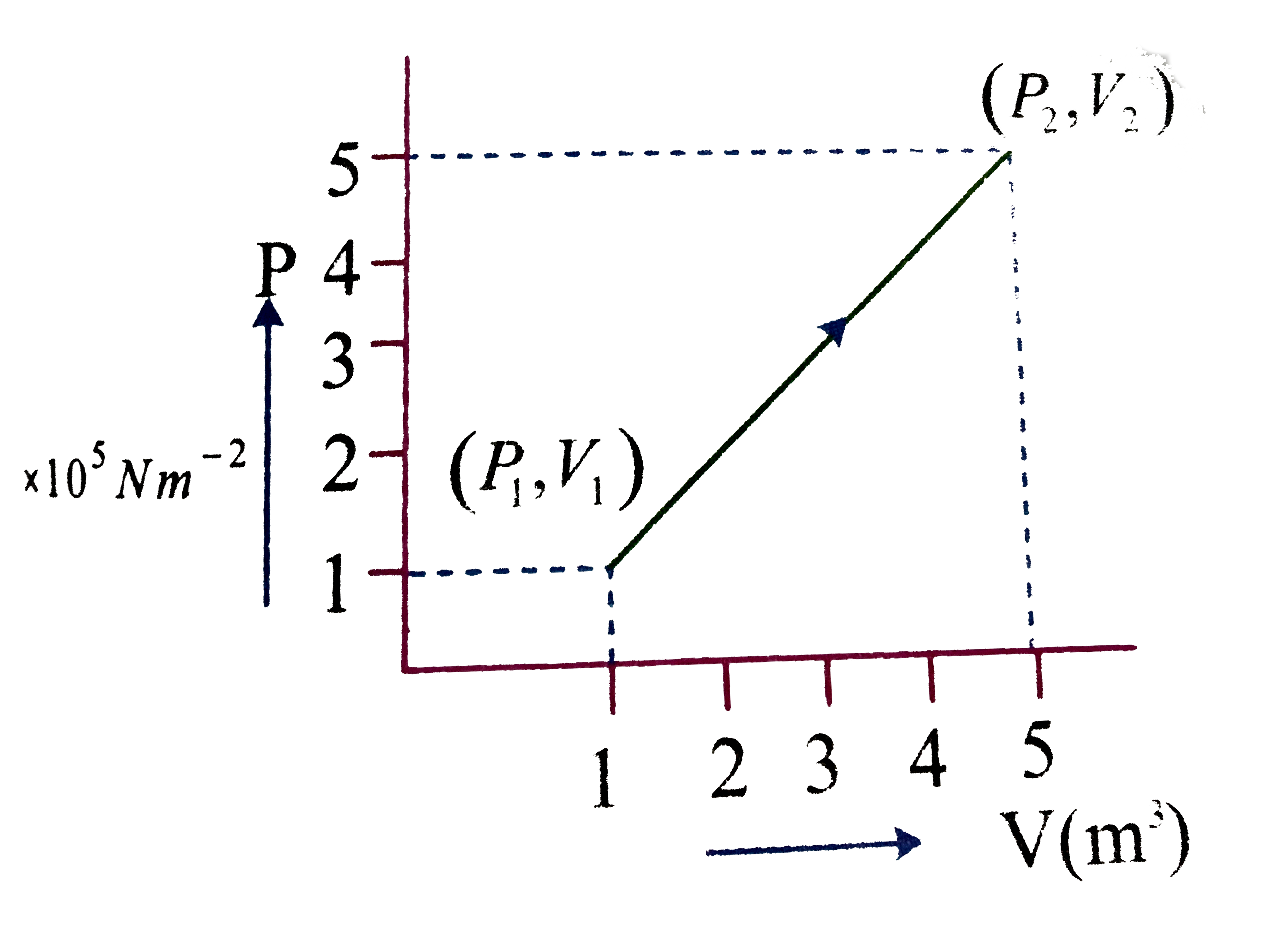
View SolutionA system changes from the state (P1,V1) to (P2,V2) as shown in the diagram. The work done by the system is
View SolutionAn ideal gas expands adiabatically from an initial temperature T1 to a final temperature T2. Prove that the work done by the gas is CV(T1−T2).
View SolutionA system can be taken from the initial state p1,V1 to the final state p2,V2 by two different methods, let ΔQandΔW represent the heat given to the system and the work done by the system. Which of the following must be the same in both the method?
View Solution
