Two coherent sources emit light of wavelength λ. Separation between them, d=4λ.
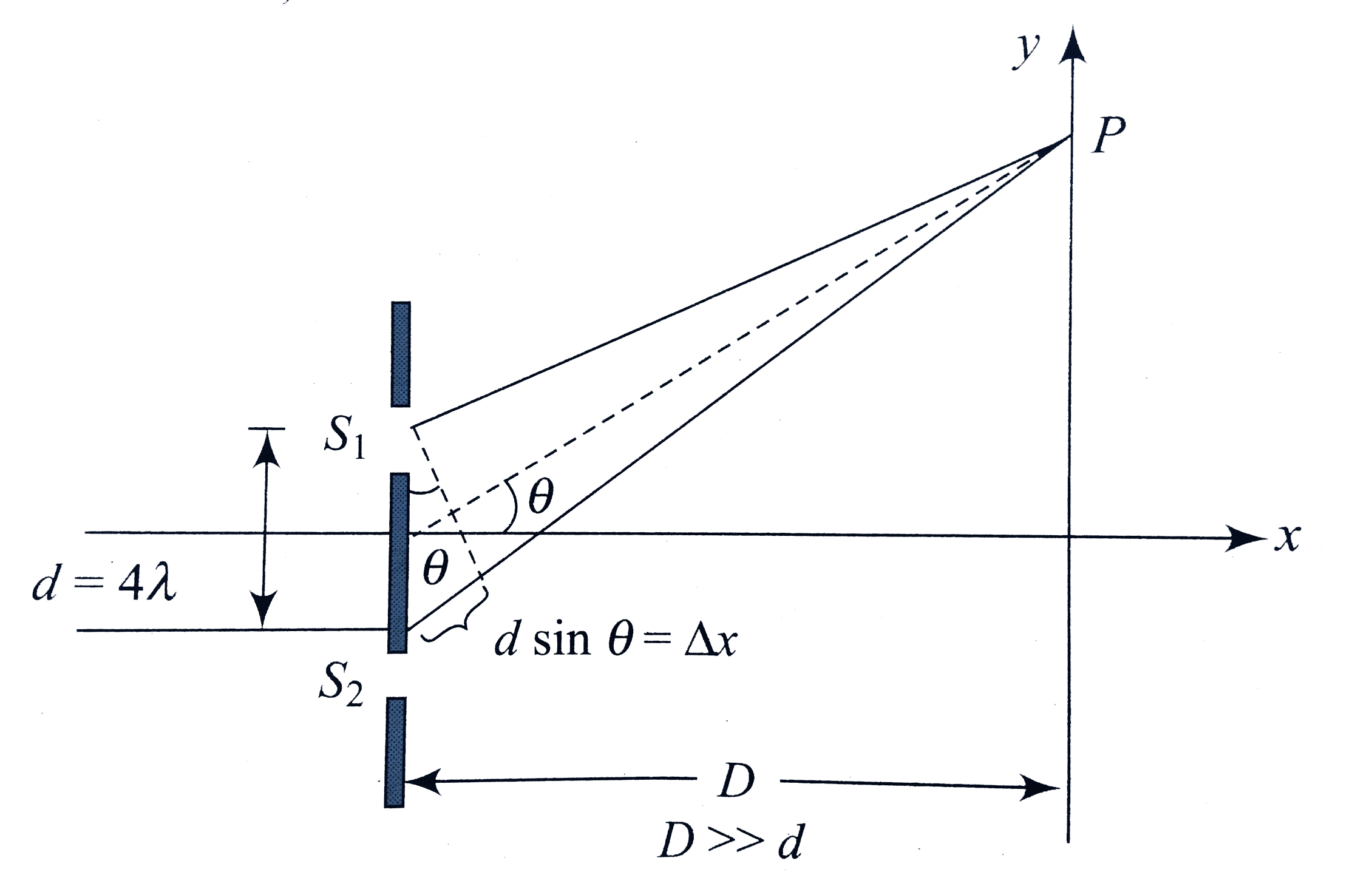
If a detector moves along the y-axis, what is the maximum number of minima observed?
6
9
5
4
The correct Answer is:b
The path difference at any point on the screen is
dsinθ=nλ
⇒n=dλsinθ
n is maximum when θ ia maximum, thus maximum value of n is
n=dλ=4
Hence, number of minima are four approximately correspondind to path difference
Δx=λ2,3λ2,5λ2,7λ2
Thus, apart from central maxima at θ=0, eight other maxima, 4 on either side of central maxima are registered. Total maxima registered are 9 and 8 minima lie between them.
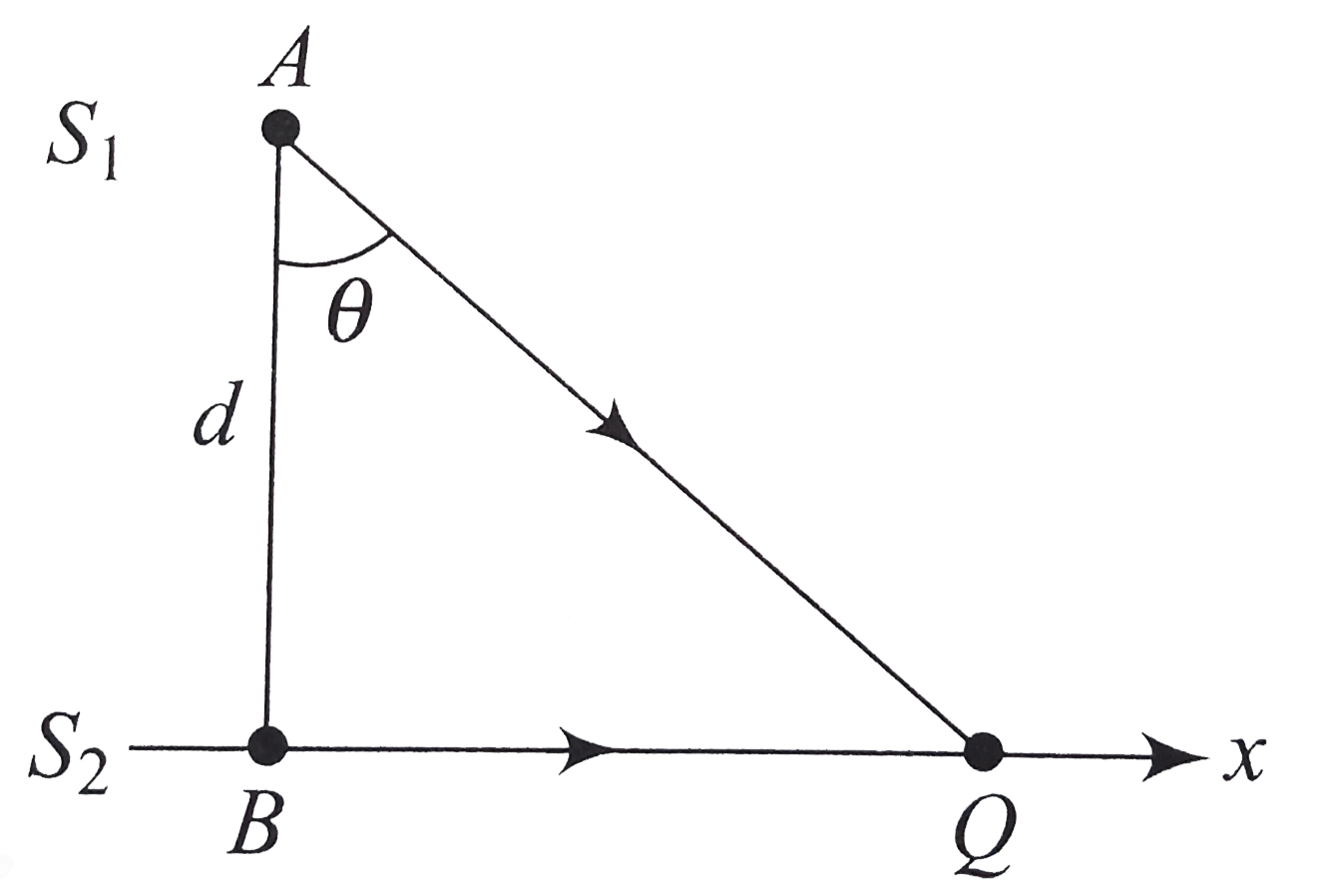
The path difference at any point Q on the x-axis is
ΔX=AQ−BQ=ABcosθ(1−sinθ)
Condition for maxima is
dcosθ(1−sinθ)=nλ
n=4(1−sinθ)cosθ
At point B, θ=0⇒n=4, i.e.,we get fourth-order maxima.
At x=∝,θ=π/2, path difference is zero
Thus, at θ=π/2, we have n=0, i.e., zeroth-order maxima is formed at x=∞.
Hence, along x-axix, beginning from slit B fifth-order maxima are registered.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives4videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
Two coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is
 View Solution
View SolutionTwo coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .View Solution
.View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
View SolutionTwo coherent light sources, each of wavelength λ, are separated by a distance 3λ, The maximum number of minima formed on line AB, which funs from −∞ to +∞, is
 View Solution
View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as
 View Solution
View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View Solution

