In the YDSE, the monochromatic source of wavelength is placed at a distance from the central axis (as shown in the figure), where d is the separation between the two slits .
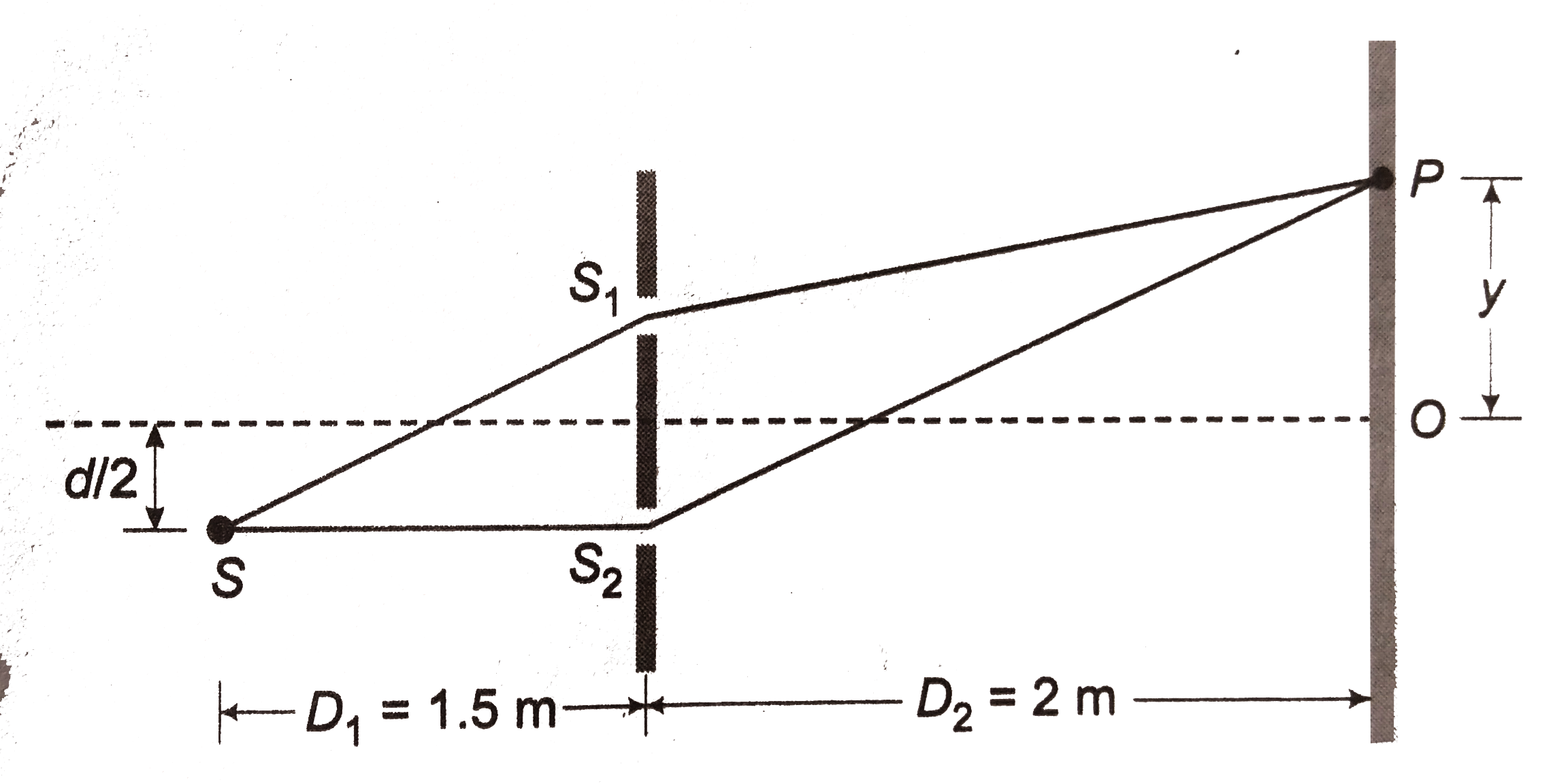
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes to be placed in front of so that intensity at O becomes th of the maximum intensity.
(Take .)
The correct Answer is:4
Step by step video & image solution for In the YDSE, the monochromatic source of wavelength lambda is placed at a distance d/2 from the central axis (as shown in the figure), where d is the separation between the two slits S_1 and S_2 . (a)Find the position of the central maxima. (b) Find the order of interference formed at O. (c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes mu =1.5 to be placed in front of S_2 so that intensity at O becomes 3/4th of the maximum intensity. (Take lambda=6000Å, d = 6mm.) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) (Straight objective Type questions)10videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) Level - II (Straight objective type questions)8videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Matrix Match Type Questions2videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)97videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
Ratio of intensities in consecutive maxima in a diffraction pattern due to a single slit is
View SolutionIn a Fraunhoffer diffraction experiment at a single slit using light of wavelength 400 nm, the first minimum is formed at an angle of 30∘ Then the direction θ of the first secondary maximum is
08:01View SolutionA double slit interference pattern is produced on a screen, as shown in the figure, using momochromatic light of wavelength 500 nm. Point P is the location of the central bright fringe, that is produced when light waves arrive in phase without any path difference. A choice of the three strips A, B and C of transparent materials with different thickness and refractive indices is available, as shown in the table. These are placed over one or both of the slits, singularly or in conjunction causing the interference pattern to be shifted across the screen from the original pattern. In the Column - I, how the strips have been placed, is mentioned whereas in the Column-II, order of the fringe at point P on the screen that will be produced due to the placement of the strip(s), is shown. Correctly match both the column.
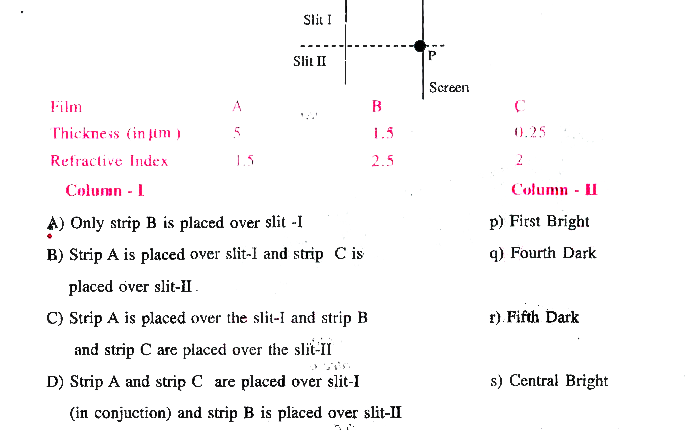 09:51View Solution
09:51View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?09:51View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train V = 330 m/s)
04:46View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 04:02View Solution
04:02View SolutionIn the YDSE, the monochromatic source of wavelength lambda is placed at a distance d/2 from the central axis (as shown in the figure), where d is the separation between the two slits S_1 and S_2 . (a)Find the position of the central maxima. (b) Find the order of interference formed at O. (c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes mu =1.5 to be placed in front of S_2 so that intensity at O becomes 3/4 th of the maximum intensity. (Take lambda=6000Å, d = 6mm .)
07:28View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
02:29View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
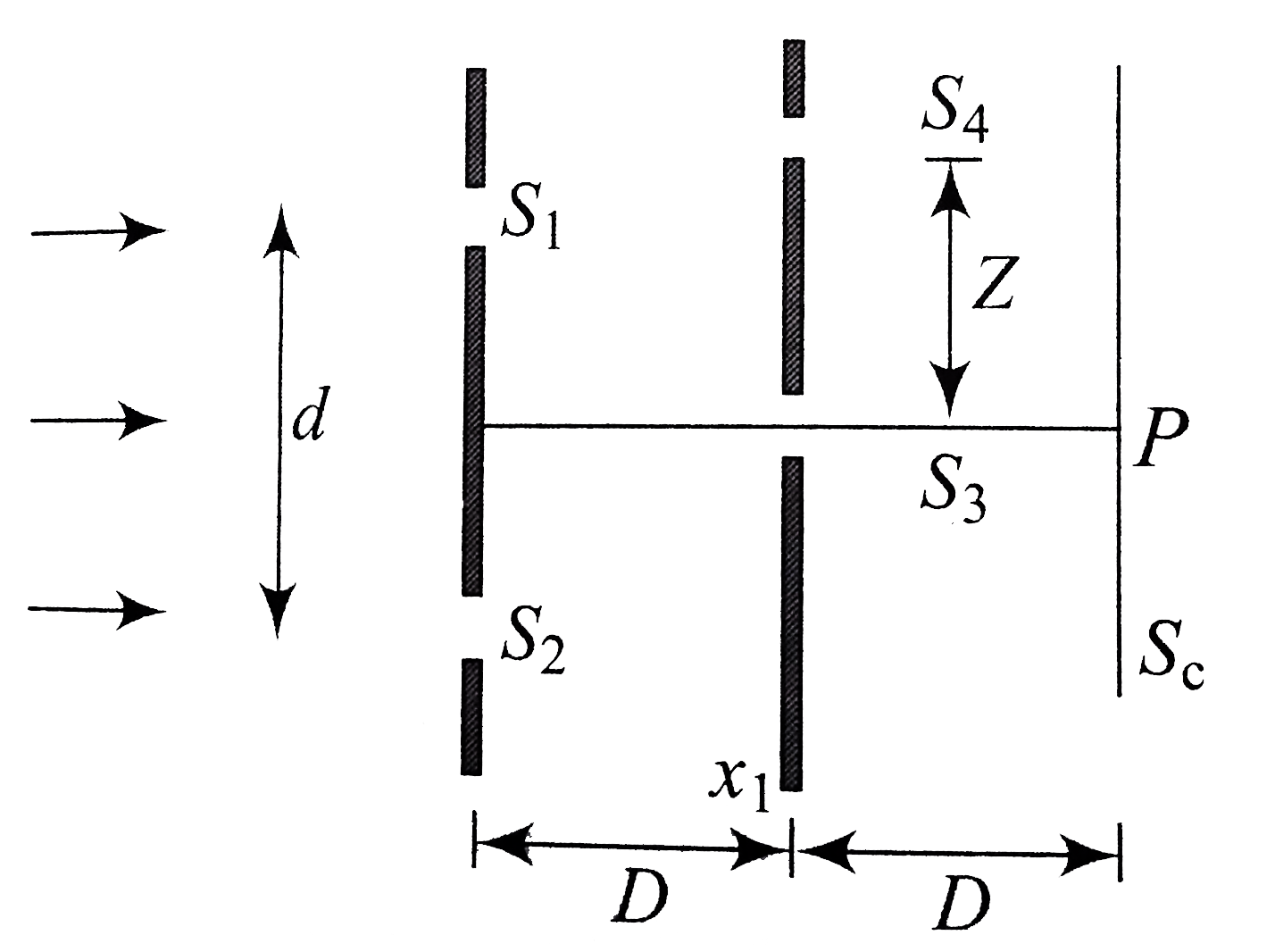
If z=λD4d04:58View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. In order to get central maxima at the centre of screen, the thickness of slab required is :
05:51View SolutionThe two coherent sources of monochromatic light of wavelength lambda are located at a separation lambda . The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
09:53View SolutionIn YDSE a = 2mm , D = 2m, lambda = 500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionIn a YDSE, D = 1m, d = 1mm and lambda = 1//2 mm Find a distance between the first and central maxima on the screen.
View SolutionIn the YDSE the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between two slits S1 and S2. Find the position of the central maxima. (Given d = 6 mm)
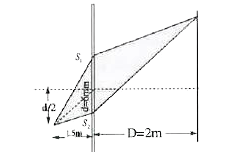 05:51View Solution
05:51View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
04:21View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 07:36View Solution
07:36View Solution

