String I and II have identical and linear mass densities, but string I is under greater tension than string II. The accompanying figure shows four different situations, A to D, in which standing wave patterns exist on the two strings. In which situation it is possible that strings I and II are oscillating at the same resonant frequency ?
_S01_009_O01.png)
_S01_009_O02.png)
_S01_009_O03.png)
_S01_009_O04.png)
The correct Answer is:C
To determine in which situation strings I and II can oscillate at the same resonant frequency, we need to analyze the relationship between tension, frequency, and wavelength for both strings.
1. Understanding the Relationship:
The frequency of a wave on a string is given by the formula:
f=12L√Tμ
where f is the frequency, L is the length of the string, T is the tension, and μ is the linear mass density of the string.
2. Identifying Given Conditions:
- Both strings I and II have identical linear mass densities (μ).
- String I is under greater tension than string II (TI>TII).
3. Analyzing Frequency:
Since the tension in string I is greater than in string II, the frequency of string I will be greater than that of string II:
fI>fII
4. Considering Wavelength:
The frequency is also inversely proportional to the wavelength (λ):
f=vλ
where v is the wave speed. For the same frequency, the wavelengths must satisfy:
λI>λII
This means that for strings I and II to have the same frequency, the wavelength of string I must be greater than that of string II.
5. Evaluating the Situations (A to D):
We need to look at the standing wave patterns in each situation (A to D) to determine where the wavelength of string I is greater than that of string II.
6. Identifying the Correct Option:
Upon examining the standing wave patterns:
- In situation C, the number of nodes and antinodes indicates that the wavelength of string I is indeed greater than that of string II, which satisfies our condition for equal frequencies.
7. Conclusion:
Therefore, the only situation where strings I and II can oscillate at the same resonant frequency is in option C.
The frequency of a wave on a string is given by the formula:
f=12L√Tμ
where f is the frequency, L is the length of the string, T is the tension, and μ is the linear mass density of the string.
- Both strings I and II have identical linear mass densities (μ).
- String I is under greater tension than string II (TI>TII).
Since the tension in string I is greater than in string II, the frequency of string I will be greater than that of string II:
fI>fII
The frequency is also inversely proportional to the wavelength (λ):
f=vλ
where v is the wave speed. For the same frequency, the wavelengths must satisfy:
λI>λII
This means that for strings I and II to have the same frequency, the wavelength of string I must be greater than that of string II.
We need to look at the standing wave patterns in each situation (A to D) to determine where the wavelength of string I is greater than that of string II.
Upon examining the standing wave patterns:
- In situation C, the number of nodes and antinodes indicates that the wavelength of string I is indeed greater than that of string II, which satisfies our condition for equal frequencies.
Therefore, the only situation where strings I and II can oscillate at the same resonant frequency is in option C.
Topper's Solved these Questions
Similar Questions
The tension, length, diameter and density of a string B are double than that of another string A. Which of the following overtones of B is same as the fundamental frequency of A?
View SolutionColumn I shows different sets of standing waves in a string of length L whose ends are fixed or free according to respective figure and Column - II shows possible equations for them where symbols have usual meaning
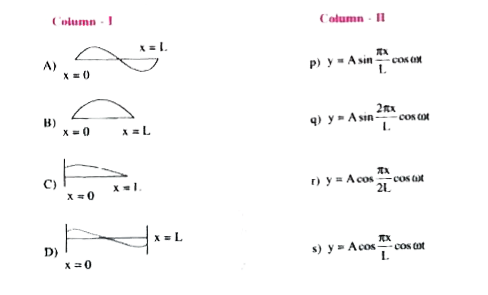View SolutionA thin taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation y(x,t)=(5.60cm)sin[(0.0340radcm)x]sin[(50.0rads)t], where the origin is at the left end of the string, the x-axis is along the string and the y-axis is perpendicular to the string.
(a) Draw a sketch that shows the standing wave pattern.
(b)Find the amplitude of the two travelling waves that make up this standing wave.
(c) What is the length of the string?
(d) Find the wavelength, frequency, period and speed of the travelling wave.
(e) Find the maximum transverse speed of a point on the string.
(f) What would be the equation y(x,t) for this string if it were vibrating in its eighth harmonic?View SolutionFigure shows different standing wave patterns on a string of linear mass density 4.0×10−2kg/m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).
View SolutionThe diagram in Fig. shows three ways in which a string of length I in an instrument can vibrate.
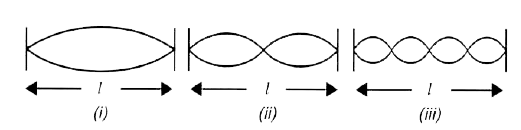
What is the ratio of frequency of vibrations in diagrams (i) and (ii) ?View SolutionTwo strings 1 and 2 are taut between two fixed supports (as shown in figure) such that the tension in both strings is same. Mass per unit length of 2 is more than that of 1. Explain which string is denser for a transverse travelling wave.
.View SolutionTwo strings 1 and 2 are taut between two fixed supports (as shown in figure) such that the tension in both strings is same. Mass per unit length of 2 is more than that of 1. Explain which string is denser for a transverse travelling wave.
.View SolutionTwo long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
View SolutionTwo strings with linear mass densities μ1=0.1kg/m and μ2=0.3kg/m are joined seamlesly. They are under tension of 20N. A travelling wave of triangular shape is moving from lighter to heavier string.
View SolutionA 2.0m long string with a linear mass density of 5.2×10−3kgm−1 and tension 52N has both of its ends fixed. It vibrates in a standing wave patten with four antinodes. Frequency of the vibraion is :-
View Solution