If the probability of a random variable X is a given below :
X=x:−2−10123P(X=x):110k152k310k
Then the value of k, is :
110
210
310
710
The correct Answer is:A
To find the value of k in the given probability distribution, we need to ensure that the sum of all probabilities equals 1. Let's break down the solution step by step.
Step 1: Write down the probabilities
The given probabilities for the random variable X are:
- P(X=−2)=110
- P(X=−1)=k
- P(X=0)=15
- P(X=1)=2k
- P(X=2)=310
- P(X=3)=k
Step 2: Set up the equation
According to the property of probability distributions, the sum of all probabilities must equal 1:
P(X=−2)+P(X=−1)+P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
Substituting the values, we get:
110+k+15+2k+310+k=1
Step 3: Simplify the equation
First, convert 15 to a fraction with a denominator of 10:
15=210
Now substitute this back into the equation:
110+k+210+2k+310+k=1
Combine like terms:
1+2+310+(k+2k+k)=1
This simplifies to:
610+4k=1
Step 4: Solve for k
Now, isolate k:
4k=1−610
Convert 1 to a fraction with a denominator of 10:
1=1010
Thus,
4k=1010−610=410
Now, divide both sides by 4:
k=410÷4=440=110
Conclusion
The value of k is 110.
---
The given probabilities for the random variable X are:
- P(X=−2)=110
- P(X=−1)=k
- P(X=0)=15
- P(X=1)=2k
- P(X=2)=310
- P(X=3)=k
According to the property of probability distributions, the sum of all probabilities must equal 1:
P(X=−2)+P(X=−1)+P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
Substituting the values, we get:
110+k+15+2k+310+k=1
First, convert 15 to a fraction with a denominator of 10:
15=210
Now substitute this back into the equation:
110+k+210+2k+310+k=1
Combine like terms:
1+2+310+(k+2k+k)=1
This simplifies to:
610+4k=1
Now, isolate k:
4k=1−610
Convert 1 to a fraction with a denominator of 10:
1=1010
Thus,
4k=1010−610=410
Now, divide both sides by 4:
k=410÷4=440=110
The value of k is 110.
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section I - Solved Mcqs
39 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test
29 Videos
Similar Questions
The probability of a random variable X is given below
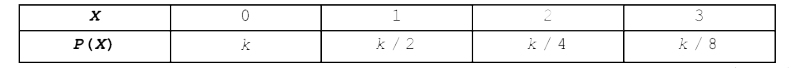
Determine the value of k
View SolutionThe probability distribution of a random variable is given below:
X=x01234567P(X=x)0k2k2k3kk22k27k2+k
Then P(0<X<5)=
View SolutionThe probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, is
View SolutionA random variable X has the following distribution
X=x1:−2−10123P(X=x1):0.1k0.22k0.3k
The value of k and its mean and variance are
View SolutionX is a random variable with distribution given below
x:0123P(X=x):k3k3kk
The value of k and its variance are
View SolutionA random variable X has the following distribution
x:1234P(X=x):k23k25k27k2
The value of k is
View SolutionA random variable X has the following distribution
X=x1:1234P(X=x1):k2k3k4k
The value of k and P(X<3) are equal to
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View Solution
