The range of random variable x={1,2,3….} and the probabilities are given by P(x=k)=3CKK! (k = 1, 2, 3, ……) and C is a constant. Then C =
log3(log2)
12log(log2)
loge(log2)loge3
log2(log3)
The correct Answer is:A
To solve the problem, we need to find the value of the constant C such that the probabilities P(x=k)=3Ckk! form a valid probability distribution. This means that the sum of all probabilities must equal 1.
1. Write the Probability Function:
The probability function is given as:
P(x=k)=3Ckk!
for k=1,2,3,…
2. Sum the Probabilities:
We need to find the sum of all probabilities:
∞∑k=1P(x=k)=∞∑k=13Ckk!
3. Recognize the Series:
The series ∞∑k=0xkk! is the Taylor series expansion for ex. Therefore, we can rewrite our sum:
∞∑k=13Ckk!=e3C−1
(Note: We start from k=1 so we subtract the k=0 term which is 1.)
4. Set the Sum Equal to 1:
For the probabilities to sum to 1, we set:
e3C−1=1
This simplifies to:
e3C=2
5. Solve for C:
Taking the natural logarithm of both sides:
3C=ln(2)
Now, we can solve for C:
C=ln(2)3
Final Answer:
Thus, the value of the constant C is:
C=ln(2)3
The probability function is given as:
P(x=k)=3Ckk!
for k=1,2,3,…
We need to find the sum of all probabilities:
∞∑k=1P(x=k)=∞∑k=13Ckk!
The series ∞∑k=0xkk! is the Taylor series expansion for ex. Therefore, we can rewrite our sum:
∞∑k=13Ckk!=e3C−1
(Note: We start from k=1 so we subtract the k=0 term which is 1.)
For the probabilities to sum to 1, we set:
e3C−1=1
This simplifies to:
e3C=2
Taking the natural logarithm of both sides:
3C=ln(2)
Now, we can solve for C:
C=ln(2)3
Thus, the value of the constant C is:
C=ln(2)3
Similar Questions
A random variable x had its range {0, 1, 2} and the probabilities are given by P(x=0)=3k3,P(x=1)=4k−10k2,P(x=2)=5k−1 where k is constant then k =
View SolutionThe range of a random variable X is {1, 2, 3, ……..} and P(X=k)=Ck⌊k where k = 1, 2, 3,…. Find the value of C
View SolutionA random variable X takes values 0, 1, 2, 3,… with probability proportional to (x+1)(15)x.
P(X≥2) equals
View SolutionA random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
View SolutionThe range of a random variable X is {0, 1, 2}. Given that P(X=0)=3c3,P(X=1)=4c−10c2,P(X=2)=5c−1 where c is constant.
Find (i) the value of c (ii) P(X<1)
(iii) P(1<X≤2) (iv) P(0<X≤3)
View SolutionThe probability of a random variable X is given below
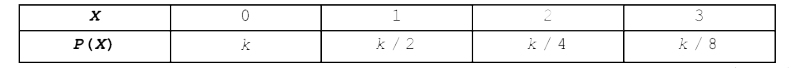
Determine the value of k
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionIf X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
View SolutionThe probability function of a random variable X is given by
p(x)=13, if x = -1, 0, 1
=0, otherwise.
Find the distribution function of X.
View SolutionIf X be a random variable taking values x1,x2,x3,….,xn with probabilities P1,P2,P3,…..Pn, respectively. Then, Var (x) is equal to …….. .
View Solution
