If S = 0, S' =0 are two touching circles then angle between their radical axis and the common tangent at the at their points of contanct is
30∘
60∘
0∘
90∘
The correct Answer is:C
To solve the problem, we need to find the angle between the radical axis of two touching circles and the common tangent at their point of contact. Let's break this down step by step.
1. Understanding the Circles:
Let the equations of the two circles be given by:
- Circle 1: S=x2+y2+2Gx+2Fy+C=0
- Circle 2: S′=x2+y2+2G′x+2F′y+C′=0
Since these circles are touching, we have S=0 and S′=0.
Hint: Identify the general form of the equations of the circles and understand what it means for them to touch.
2. Finding the Common Tangent:
The equation of the common tangent to the two circles can be derived from the condition that the distance from the center of each circle to the tangent is equal to their respective radii. The equation can be expressed as:
S−S′=0
This leads to:
(2G−2G′)x+(2F−2F′)y+(C−C′)=0
Hint: Remember that the common tangent can be derived from the difference of the equations of the circles.
3. Finding the Radical Axis:
The radical axis of two circles is given by the equation:
S−S′=0
which is the same as the equation for the common tangent derived above.
Hint: The radical axis is the locus of points that have equal power with respect to both circles.
4. Analyzing the Equations:
Since both the common tangent and the radical axis have the same equation:
(2G−2G′)x+(2F−2F′)y+(C−C′)=0
This indicates that they coincide.
Hint: If two lines are represented by the same equation, they are the same line.
5. Conclusion on the Angle:
Since the radical axis and the common tangent coincide, the angle between them is 0∘.
Final Answer: The angle between the radical axis and the common tangent at their point of contact is 0∘.
Let the equations of the two circles be given by:
- Circle 1: S=x2+y2+2Gx+2Fy+C=0
- Circle 2: S′=x2+y2+2G′x+2F′y+C′=0
Since these circles are touching, we have S=0 and S′=0.
The equation of the common tangent to the two circles can be derived from the condition that the distance from the center of each circle to the tangent is equal to their respective radii. The equation can be expressed as:
S−S′=0
This leads to:
(2G−2G′)x+(2F−2F′)y+(C−C′)=0
The radical axis of two circles is given by the equation:
S−S′=0
which is the same as the equation for the common tangent derived above.
Since both the common tangent and the radical axis have the same equation:
(2G−2G′)x+(2F−2F′)y+(C−C′)=0
This indicates that they coincide.
Since the radical axis and the common tangent coincide, the angle between them is 0∘.
Similar Questions
Knowledge Check
The angle between the tangents to the curve y=x2−5x+6 at the point (2,0) and (3,0) is
Aπ2Bπ3Cπ6Dπ4
The circles x2+y2−2x−4y+1=0 and x2+y2+4x+4y−1=0 ............a)touch internally b)touch externally c)have 3x+4y−1=0 as the common tangent at the point of contact d)have 3x+4y+1=0 as the common tangent at the point of contact
View SolutionThe circles x2+y2−2x−4y+1=0 and x2+y2+4x+4y−1=0 (a)touch internally (b)touch externally (c)have 3x+4y−1=0 as the common tangent at the point of contact have 3x+4y+1=0 (d)as the common tangent at the point of contact
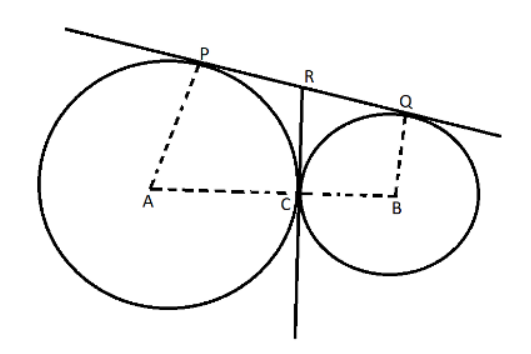
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionStatement 1 : The number of common tangents to the circles x2+y2−x=0 and x2+y2+x=0 is 3.
Statement 2 : If two circles touch each other externally then it has two direct common tangents and one indirect common tangent.
View SolutionTwo circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .
View SolutionTwo circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .
View Solution
