Four persons A, B, C and D initially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always, the person will meet after time
dv
√2dv
d2v
d√2v
The correct Answer is:A
To solve the problem of four persons A, B, C, and D starting at the corners of a square and moving towards each other while always facing one another, we can follow these steps:
Step 1: Understand the Configuration
We have a square with side length d. The four persons are positioned at the corners of the square:
- A at (0, 0)
- B at (d, 0)
- C at (d, d)
- D at (0, d)
Step 2: Determine the Movement Direction
Each person moves towards the person they are facing. Since they are always facing each other, they will move in a curved path towards the center of the square.
Step 3: Calculate the Distance to the Center
The center of the square can be found at the coordinates:
(d2,d2)
The distance from any corner (say A) to the center is given by:
Distance=√(d2−0)2+(d2−0)2=√(d2)2+(d2)2=√d24+d24=√d22=d√2
Step 4: Relate Distance, Speed, and Time
Each person moves with a constant speed v. The time T taken to reach the center can be calculated using the formula:
T=DistanceSpeed=d√2v=dv√2
Conclusion
Thus, the time taken for all four persons to meet at the center of the square is:
T=dv√2
We have a square with side length d. The four persons are positioned at the corners of the square:
- A at (0, 0)
- B at (d, 0)
- C at (d, d)
- D at (0, d)
Each person moves towards the person they are facing. Since they are always facing each other, they will move in a curved path towards the center of the square.
The center of the square can be found at the coordinates:
(d2,d2)
The distance from any corner (say A) to the center is given by:
Distance=√(d2−0)2+(d2−0)2=√(d2)2+(d2)2=√d24+d24=√d22=d√2
Each person moves with a constant speed v. The time T taken to reach the center can be calculated using the formula:
T=DistanceSpeed=d√2v=dv√2
Thus, the time taken for all four persons to meet at the center of the square is:
T=dv√2
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A STRAIGHT LINE
59 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Four persons K,L,M,N are initially at the four corners of a square of side d. Each person now moves with a uniform speed v in such a way that K always moves directly towards L, L directly towards M, M directly towards N, and N directly towards K. The four persons will meet at a time............. .
View SolutionFour particles A,B,CandD are situated at the corner of a square ABCD of side a at t-0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CD~andD along DA. At what time will these particles meet each other ?
View Solution
Knowledge Check
Four children are standing at the corners A, B, C and D of a square of side l. They simultaneously start running such that A runs towards B, B towaards C, C runs towards D and D runs towards A, each with a velocity v.They will meet after a time
 A√2l/vBl/vCl/√2vD4l/v
A√2l/vBl/vCl/√2vD4l/vTwo short bar magnets of magnetic moments m each are arranged at the opposite corners of a square of side d such that their centres coincide with thecorners and their axes are parallel. If the like poles are in the same direction, the magnetic induction at any of the other corners of the square is
Aμ04πmd3Bμ04π2md3Cμ04πm2d3Dμ04πm32d3
Four charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View Solution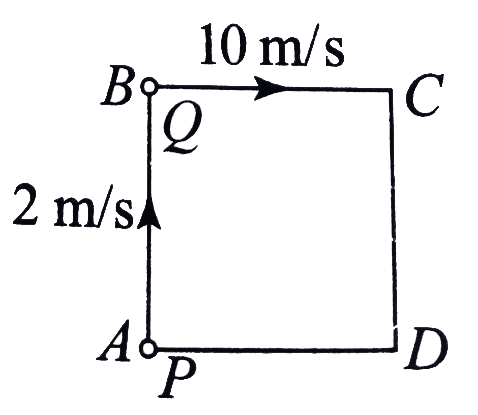
Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2m/s and 10m/s respectively. Find the time when they will meet for the first time
View Solution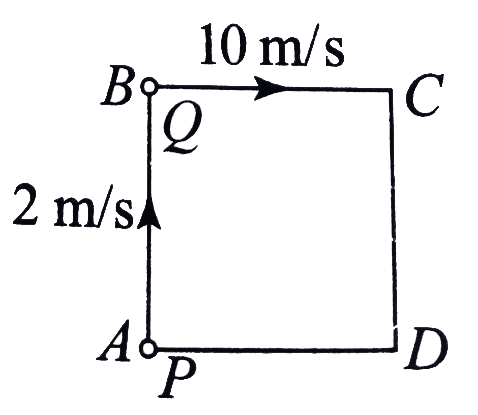
Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2ms and 10ms respectively. Find the time when they will meet for the first time
View SolutionFor charges A,B,C and D are plasced at the four corners of a squre of a side a. The energy required to take the charges C and D to infinity (they are also infinitely separated from each other )is

View SolutionFive persons A, B, C, D and E are pulling a cart of mass 100 kg on a smooth surface and the cart is moving with an acceleration of 3ms−2 in the east direction. If another person F comes and ans starts pulling the cart with a force of 100 N due west , then the acceleration of the cart will be
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View Solution