A vertical disc has three grooves directed along chords AB, AC and AD. Three bodies begin to slide down the respective grooves from A simultaneously. If AB > AC > AD, the respective time intervals to reach the bottoms of the respective grooves t1,t2andt3 are
t1>t2>t3
t1<t2<t3
t1>t2<t3
t1=t2=t3
The correct Answer is:D
To solve the problem, we need to analyze the motion of the bodies sliding down the grooves of the vertical disc. Let's break down the solution step by step:
Step 1: Understand the Setup
We have a vertical disc with three grooves (AB, AC, and AD) that are directed along chords of the disc. The lengths of the grooves are given as AB>AC>AD.
Step 2: Identify the Forces Acting on the Bodies
As the bodies slide down the grooves, the only force acting on them is gravity. The effective acceleration along each groove can be expressed as:
a=gcosθ
where g is the acceleration due to gravity and θ is the angle of the groove with respect to the vertical.
Step 3: Determine the Length of Each Groove
The length of each groove can be represented as:
- For groove AB: L1=2Rcosθ1
- For groove AC: L2=2Rcosθ2
- For groove AD: L3=2Rcosθ3
Given that AB>AC>AD, we can infer that θ1<θ2<θ3.
Step 4: Apply the Kinematic Equation
Using the kinematic equation:
S=ut+12at2
Since the bodies start from rest, u=0, and the equation simplifies to:
S=12at2
Step 5: Substitute for Each Groove
For each groove, we can substitute the respective lengths and accelerations:
1. For groove AB:
L1=12(gcosθ1)t21
Rearranging gives:
t21=2L1gcosθ1
2. For groove AC:
L2=12(gcosθ2)t22
Rearranging gives:
t22=2L2gcosθ2
3. For groove AD:
L3=12(gcosθ3)t23
Rearranging gives:
t23=2L3gcosθ3
Step 6: Analyze the Time Intervals
From the equations derived, we can see that the time taken for each body to reach the bottom depends on the length of the groove and the angle. However, since the acceleration due to gravity g and the factor of 2g is constant for all grooves, the time intervals t1,t2,t3 will depend primarily on the cosine of the angles.
Step 7: Conclusion
Since the angles θ1,θ2,θ3 will affect the time taken, and given that AB>AC>AD implies that θ1<θ2<θ3, we can conclude:
- t1<t2<t3
Thus, the respective time intervals to reach the bottoms of the respective grooves are:
t1<t2<t3
We have a vertical disc with three grooves (AB, AC, and AD) that are directed along chords of the disc. The lengths of the grooves are given as AB>AC>AD.
As the bodies slide down the grooves, the only force acting on them is gravity. The effective acceleration along each groove can be expressed as:
a=gcosθ
where g is the acceleration due to gravity and θ is the angle of the groove with respect to the vertical.
The length of each groove can be represented as:
- For groove AB: L1=2Rcosθ1
- For groove AC: L2=2Rcosθ2
- For groove AD: L3=2Rcosθ3
Using the kinematic equation:
S=ut+12at2
Since the bodies start from rest, u=0, and the equation simplifies to:
S=12at2
For each groove, we can substitute the respective lengths and accelerations:
1. For groove AB:
L1=12(gcosθ1)t21
Rearranging gives:
t21=2L1gcosθ1
L2=12(gcosθ2)t22
Rearranging gives:
t22=2L2gcosθ2
L3=12(gcosθ3)t23
Rearranging gives:
t23=2L3gcosθ3
From the equations derived, we can see that the time taken for each body to reach the bottom depends on the length of the groove and the angle. However, since the acceleration due to gravity g and the factor of 2g is constant for all grooves, the time intervals t1,t2,t3 will depend primarily on the cosine of the angles.
Since the angles θ1,θ2,θ3 will affect the time taken, and given that AB>AC>AD implies that θ1<θ2<θ3, we can conclude:
- t1<t2<t3
t1<t2<t3
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A STRAIGHT LINE
59 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A ball is thrown vertically upwards from the ground. If T1 and T2 are the respective time taken in going up and coming down, and the air resistance is not ignored, then
View SolutionFrom the top of a tower, a stone is thrown up and it reaches the ground in time t1A second stone is thrown down with the same speed and it reaches the ground in time t2 A third stone is released from rest and it reaches the ground in time The correct relation between t1,t2 and t3 is :
View SolutionA disc in which serval grooves are cut along the chord drawn from a point 'A', is arranged in a vertical plane several particles starts slipping from 'A' along the grooves simultaneously. Assuming friction and resistance negligible, the time taken in reaching the edge of disc will be :-

View SolutionABC is isosceles triangle, right angled at A. The resultant of the forces acting along −−→AB,−−→AC with magnitudes 1AB and 1AC respectively is the force along −−→AD, where D is the foot of the perpendicular from A on BC. The magnitude of the resultant is:
View SolutionA stone thrown vertically up with velocity v reaches three points A, B and C with velocities v,v2 and v4 respectively. Then AB:BC is
View SolutionA man directly crosses a river in time t1 and swims down the current a distance equal to the width of the river I time t2. If uandv be the speed of the current and the man respectively, show that : t1:t2=√v+u:√v−u).
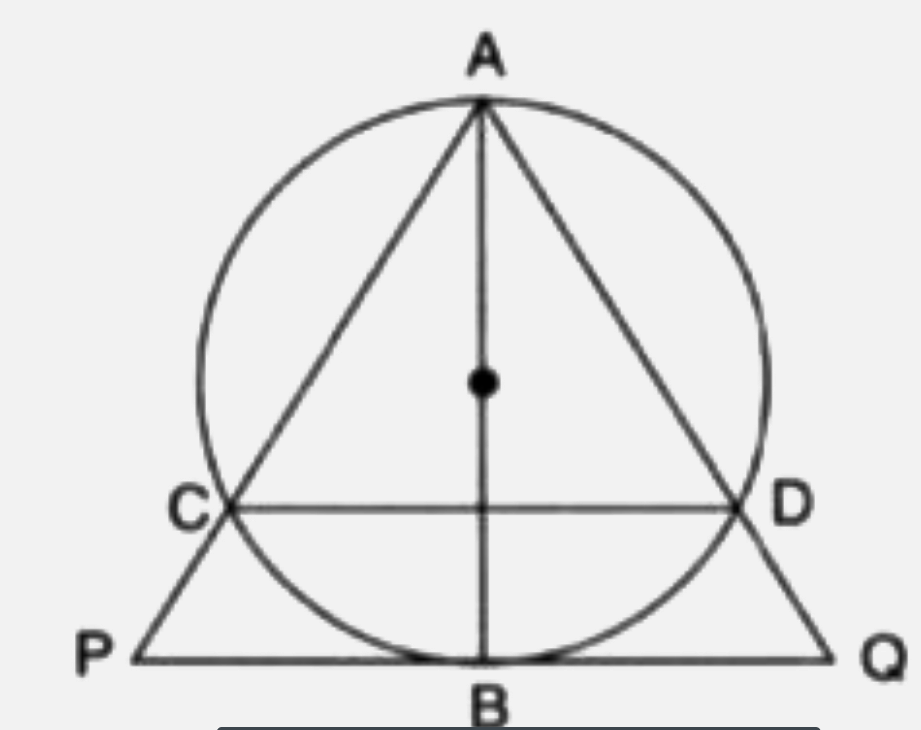
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionAssertion : A ring and a disc of same mass and radius begin to roll without slipping from the top of an inclined surface at t=0. The ring reaches the bottom of incline in time t1 while the disc reaches the bottom in time t2, then t1<t2
Reason : Disc will roll down tha plane with more acceleration because of its lesser value of moment of inertia.
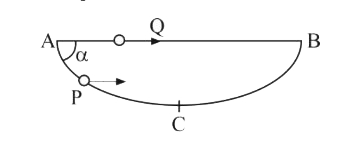
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t = 0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t = 0 along the horizontal string AB, with a speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:
View Solution
