A block of mass 10kg pushed by a horizontal force F on a horizontal rough plane moves with an aceleration 5ms−2. When force is doubled, its acceleration becomes 18ms−2. The coefficient of friction is (g=10ms−2)
0.8
0.2
0.4
0.6
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the block and use Newton's second law of motion. Let's break it down step by step.
Step 1: Identify the known values
- Mass of the block, m=10kg
- Initial acceleration, a1=5m/s2
- Final acceleration when force is doubled, a2=18m/s2
- Gravitational acceleration, g=10m/s2
Step 2: Calculate the normal force
The normal force N acting on the block is equal to the weight of the block, which is given by:
N=mg=10kg×10m/s2=100N
Step 3: Write the equations of motion for both cases
1. First case (force F and acceleration a1):
The net force acting on the block can be expressed as:
F−f=ma1
where f is the frictional force. The frictional force can be expressed as:
f=μN
Substituting N:
F−μN=ma1⟹F−μ(100)=10(5)⟹F−100μ=50(Equation 1)
2. Second case (force 2F and acceleration a2):
The net force in this case is:
2F−f=ma2
Substituting for f:
2F−μN=ma2⟹2F−μ(100)=10(18)⟹2F−100μ=180(Equation 2)
Step 4: Solve the equations
Now we have two equations:
1. F−100μ=50 (Equation 1)
2. 2F−100μ=180 (Equation 2)
To eliminate μ, we can subtract Equation 1 from Equation 2:
(2F−100μ)−(F−100μ)=180−50
This simplifies to:
2F−F=130⟹F=130N
Step 5: Substitute F back to find μ
Now substitute F=130N back into Equation 1:
130−100μ=50
Rearranging gives:
100μ=130−50⟹100μ=80⟹μ=0.8
Conclusion
The coefficient of friction μ is:
μ=0.8
- Mass of the block, m=10kg
- Initial acceleration, a1=5m/s2
- Final acceleration when force is doubled, a2=18m/s2
- Gravitational acceleration, g=10m/s2
The normal force N acting on the block is equal to the weight of the block, which is given by:
N=mg=10kg×10m/s2=100N
1. First case (force F and acceleration a1):
The net force acting on the block can be expressed as:
F−f=ma1
where f is the frictional force. The frictional force can be expressed as:
f=μN
Substituting N:
F−μN=ma1⟹F−μ(100)=10(5)⟹F−100μ=50(Equation 1)
The net force in this case is:
2F−f=ma2
Substituting for f:
2F−μN=ma2⟹2F−μ(100)=10(18)⟹2F−100μ=180(Equation 2)
Now we have two equations:
1. F−100μ=50 (Equation 1)
2. 2F−100μ=180 (Equation 2)
(2F−100μ)−(F−100μ)=180−50
This simplifies to:
2F−F=130⟹F=130N
Now substitute F=130N back into Equation 1:
130−100μ=50
Rearranging gives:
100μ=130−50⟹100μ=80⟹μ=0.8
The coefficient of friction μ is:
μ=0.8
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A body of mass 10 kg lies on a rough horizontal surface. When a horizontal force of F newtons acts on it, it gets an acceleration of 5m/s2. And when the horizontal force is doubled, it gets an acceleration of 18m/s2. The coefficient of friction between the body and the horizontal surface is
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
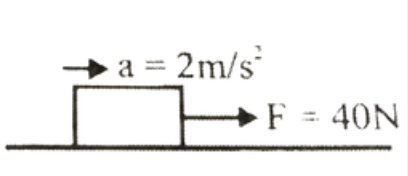
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View SolutionA balloon of mass 10 kg is raising up with an acceleration of 20ms−2. If a mass of 4 kg is removed from the balloon its acceleration becomes ( take, g=10ms−2)
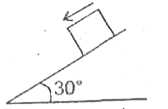
View SolutionA block of mass 10 kg is released on rough incline plane. Block start descending with acceleration 2m/s2. Kinetic friction force acting on block is (take g=10m/s2)
View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA horizontal force of 150N produces an acceleration of 2m/s2 in a body placed on a 6 horizontal surface. A horizontal force of 200N produces an acceleration of 3m/s2. The mass of the body and coefficient of kinetic friction are (g = 10 ms−2)
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. If the coefficient of static & kinetic friction are 0.4 & 0.3, the frictional force acting on the block is: (g=10ms−2)
View SolutionA block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionA block of 10kg is pulled at a constant speed on a rough horizontal plane by a force of 20N. Calculate the coefficient of friction ?
View Solution
