A condenser is charged using a constant current. The ratio of the magnetic fields at a distance of R/2 and R from the axis is (R is the radius of plate )
1:1
2:1
1:2
1:4
To solve the problem of finding the ratio of the magnetic fields at distances R/2 and R from the axis of a charged condenser, we can follow these steps:
Step 1: Understand the Magnetic Field Due to a Current
The magnetic field B around a long straight conductor carrying a current I at a distance r from the axis can be expressed using Ampere's Law:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 2: Calculate Magnetic Field at Distance R/2
For the first case, we need to find the magnetic field B1 at a distance r=R/2:
B1=μ0I2π(R/2)=μ0IπR
Step 3: Calculate Magnetic Field at Distance R
Now, for the second case, we find the magnetic field B2 at a distance r=R:
B2=μ0I2πR
Step 4: Find the Ratio of the Magnetic Fields
Now, we can find the ratio of the magnetic fields B1B2:
B1B2=μ0IπRμ0I2πR=1πR12πR=21=2
Conclusion
Thus, the ratio of the magnetic fields at distances R/2 and R from the axis is:
B1B2=2
Final Answer
The ratio of the magnetic fields at a distance of R/2 and R is 2:1.
---
The magnetic field B around a long straight conductor carrying a current I at a distance r from the axis can be expressed using Ampere's Law:
B=μ0I2πr
where μ0 is the permeability of free space.
For the first case, we need to find the magnetic field B1 at a distance r=R/2:
B1=μ0I2π(R/2)=μ0IπR
Now, for the second case, we find the magnetic field B2 at a distance r=R:
B2=μ0I2πR
Now, we can find the ratio of the magnetic fields B1B2:
B1B2=μ0IπRμ0I2πR=1πR12πR=21=2
Thus, the ratio of the magnetic fields at distances R/2 and R from the axis is:
B1B2=2
The ratio of the magnetic fields at a distance of R/2 and R is 2:1.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -IB37videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE13videos
ELECTROMAGNETICS
Similar Questions
A cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View Solution
Knowledge Check
- Question 1 - Select One
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A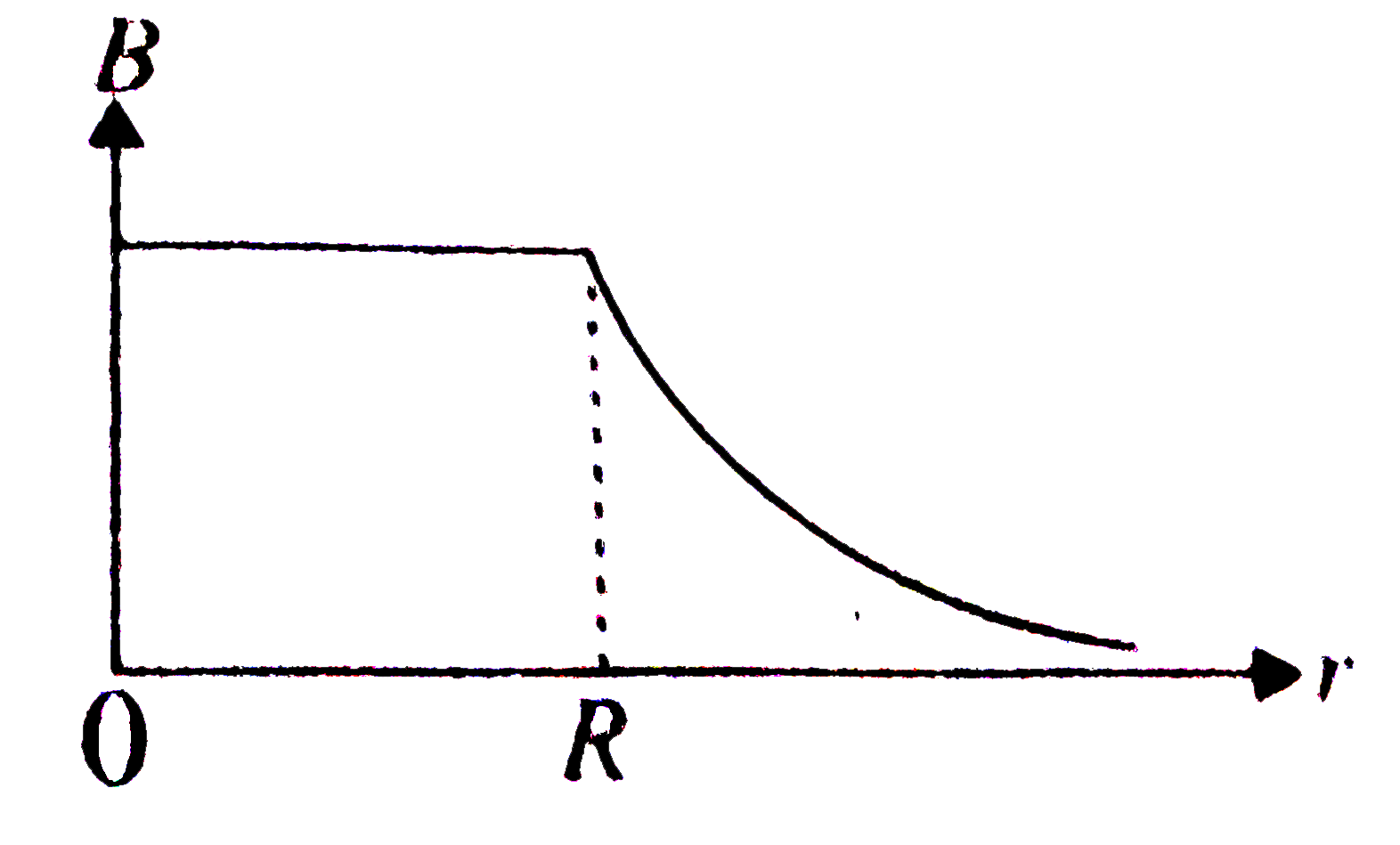 B
B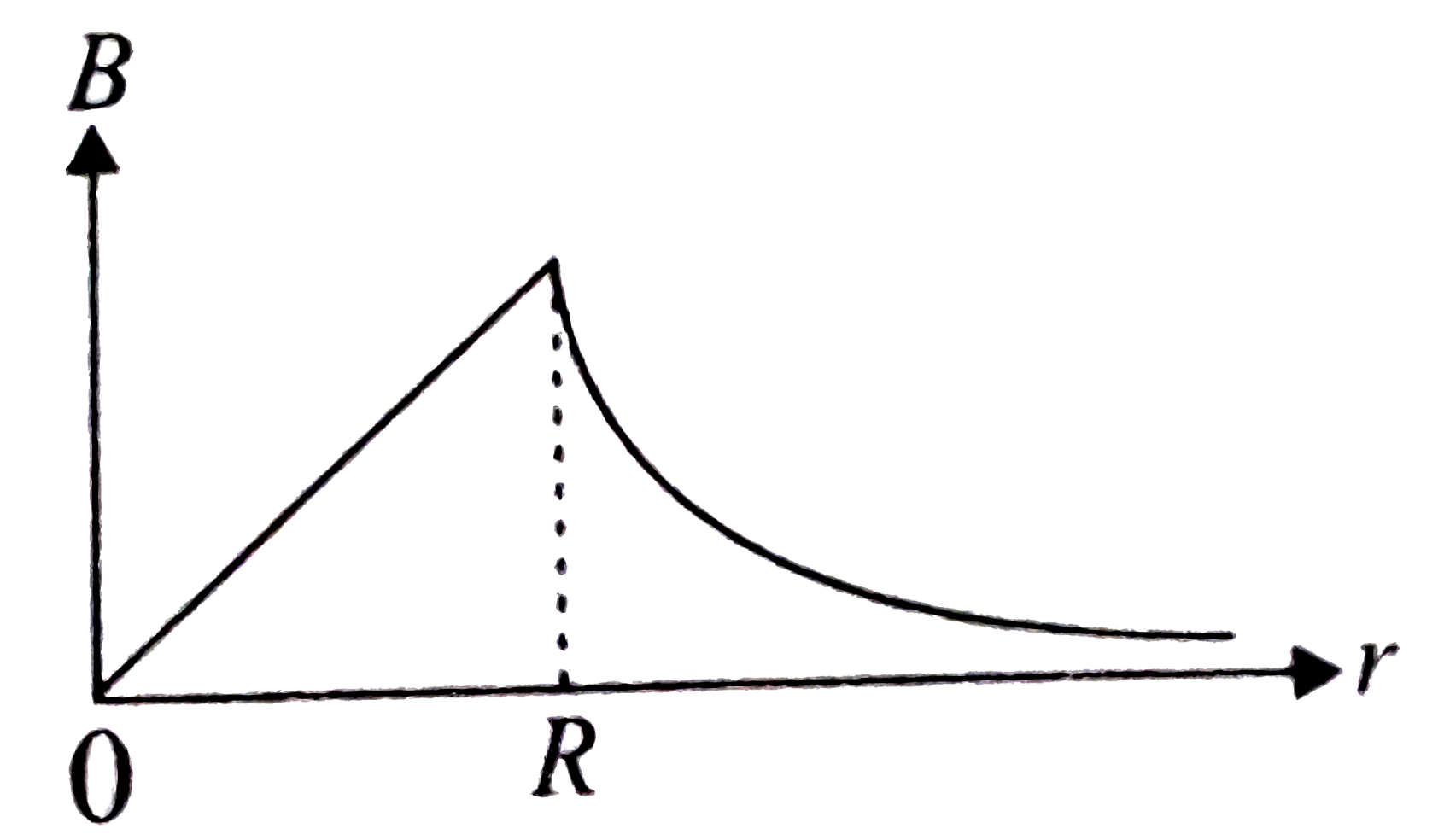 C
C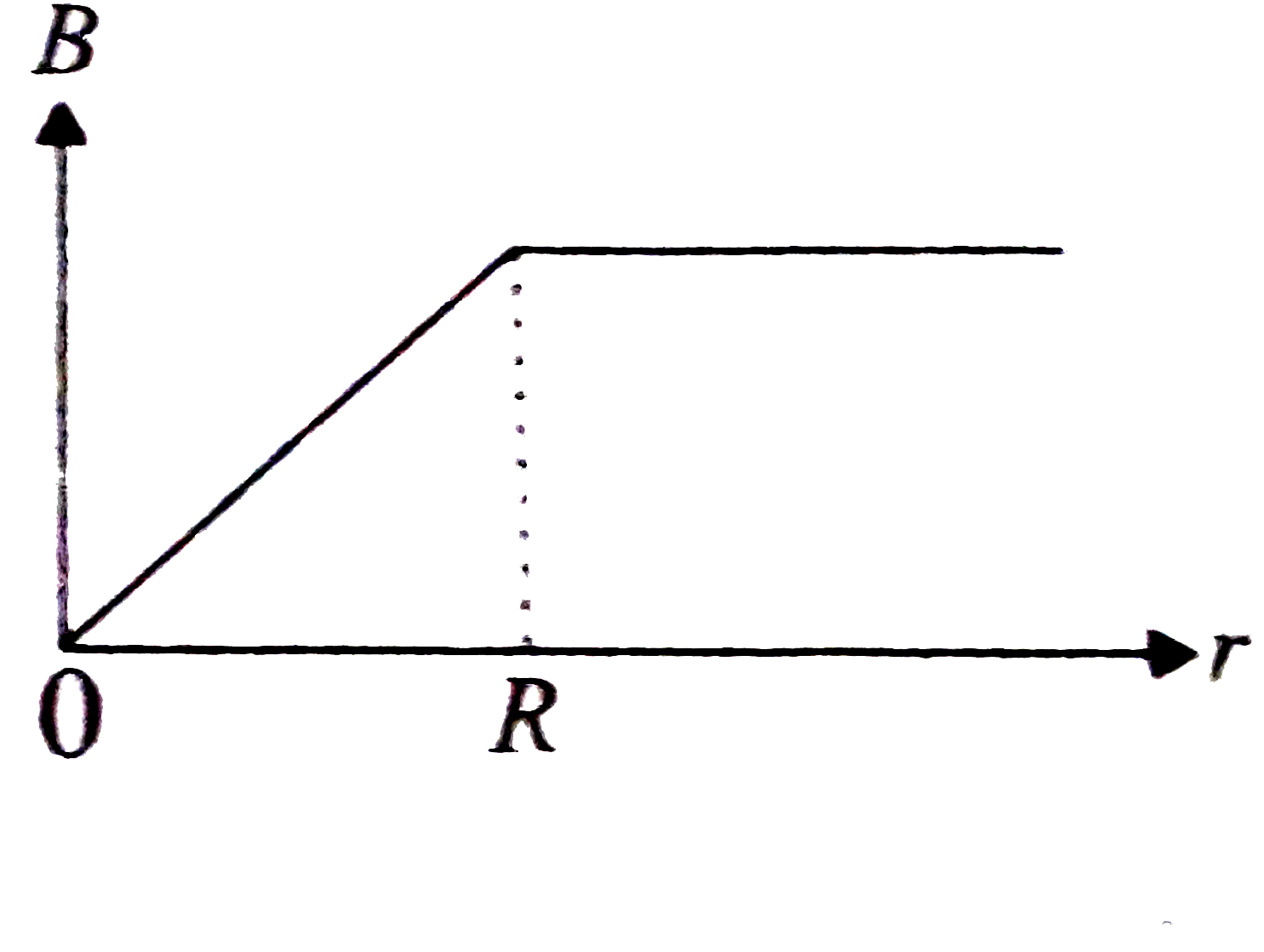 D
D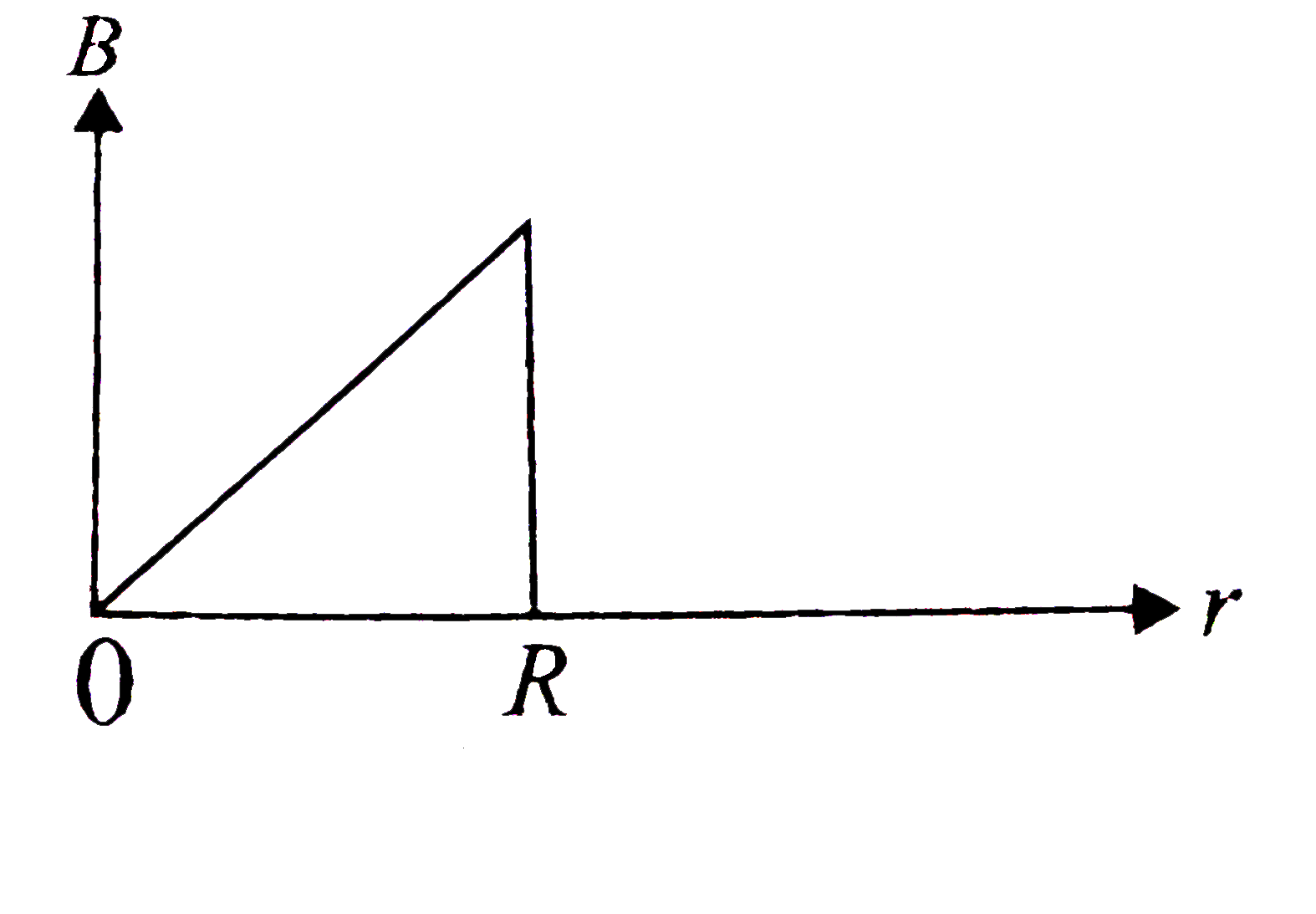
A sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionConsider an infinitely long current carrying cylindrical straight wire having radius 'a'. Then the ratio of magnetic field at distance a3 and 2a from axis of wire is.
View SolutionConsider an infinitely long current carrying cylindrical straight wire having radius 'a'. Then the ratio of magnetic field at distance a3 and 2a from axis of wire is.
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionSuppose that the current density in a wire of radius a varius with r according to Kr2 where K is a constant and r is the distance from the axis of the wire. Find the magnetic field at a point at distance r form the axis when (a) r<a and (b) r>a.
View SolutionA cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution

