A charged bead is capable of sliding freely through a string held vertically in tension. An electric field is applied parallel to the string so that the bead stays at rest of the middle of the string. If the electric field is switched off momentarily and switched on
the bead moves downwards and stops as soon as the field is switched on
the bead moved downwards when the field is switched off and moves upwards when the field is switched on
the bead moves downwards with constant acceleration till it reaches the bottom of the string
the bead moves downwards with constant velocity till it reaches the bottom of the string
The correct Answer is:D
To solve the problem, we need to analyze the behavior of the charged bead when the electric field is switched off and then switched back on. Here’s a step-by-step solution:
Step 1: Understand the Initial Condition
The charged bead is at rest in the middle of the string due to the balance of forces. The electric force acting on the bead (due to the electric field) is equal to the gravitational force acting on it.
Hint: Remember that the forces acting on the bead are balanced when it is at rest.
Step 2: Write the Force Balance Equation
When the bead is at rest, we can write the equation:
E⋅Q=mg
Where:
- E is the electric field strength,
- Q is the charge of the bead,
- m is the mass of the bead,
- g is the acceleration due to gravity.
Hint: This equation shows that the electric force equals the weight of the bead.
Step 3: Analyze the Situation When the Electric Field is Switched Off
When the electric field is switched off momentarily, the only force acting on the bead is the gravitational force mg. The bead will start to accelerate downwards due to gravity.
Hint: Think about how the bead will behave when only gravity is acting on it.
Step 4: Calculate the Velocity of the Bead
Since the bead starts from rest, we can use the equation of motion to find its velocity after a time t:
v=u+gt
Where:
- u=0 (initial velocity),
- v is the final velocity after time t.
Thus, we have:
v=gt
Hint: The bead accelerates downwards under gravity, so its velocity increases linearly with time.
Step 5: Analyze the Situation When the Electric Field is Switched On Again
When the electric field is switched back on, the electric force will act on the bead again. However, at this moment, the bead has a downward velocity v=gt. The electric force will now balance the gravitational force, but since the bead already has downward velocity, it will continue moving downwards.
Hint: Consider what happens to the forces acting on the bead when the electric field is reapplied.
Step 6: Determine the Motion of the Bead
Since the electric force re-establishes the balance with the gravitational force, the net force on the bead becomes zero. Therefore, the bead will move downwards with a constant velocity gt until it reaches the bottom of the string.
Hint: Remember that constant velocity means no net acceleration.
Final Conclusion
The correct answer is that the bead moves downwards with constant velocity until it reaches the bottom of the string.
Answer:
Option 4: The bead moves downwards with constant velocity till it reaches the bottom of the string.
The charged bead is at rest in the middle of the string due to the balance of forces. The electric force acting on the bead (due to the electric field) is equal to the gravitational force acting on it.
When the bead is at rest, we can write the equation:
E⋅Q=mg
Where:
- E is the electric field strength,
- Q is the charge of the bead,
- m is the mass of the bead,
- g is the acceleration due to gravity.
When the electric field is switched off momentarily, the only force acting on the bead is the gravitational force mg. The bead will start to accelerate downwards due to gravity.
Since the bead starts from rest, we can use the equation of motion to find its velocity after a time t:
v=u+gt
Where:
- u=0 (initial velocity),
- v is the final velocity after time t.
v=gt
When the electric field is switched back on, the electric force will act on the bead again. However, at this moment, the bead has a downward velocity v=gt. The electric force will now balance the gravitational force, but since the bead already has downward velocity, it will continue moving downwards.
Since the electric force re-establishes the balance with the gravitational force, the net force on the bead becomes zero. Therefore, the bead will move downwards with a constant velocity gt until it reaches the bottom of the string.
The correct answer is that the bead moves downwards with constant velocity until it reaches the bottom of the string.
Option 4: The bead moves downwards with constant velocity till it reaches the bottom of the string.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-II56videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assess Your Self13videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX42videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
Similar Questions
A particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
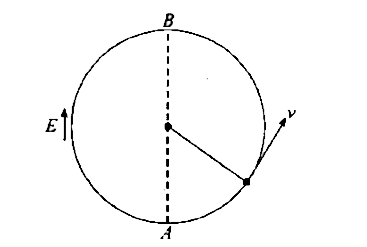 View Solution
View SolutionA charged ball of mass m and charge q is projected from the ground with an initail velocity u and angle of projection θ at the time of projection vertically upward electric field E is switched on. When it reaches the maximum height electric filed is switched off and a horizontal electric feild of same magnitude E is switched on. Then answer the following question (Assume mg> qE)
Q In the above experimentView SolutionA charged ball of mass m and charge q is projected from the ground with an initail velocity u and angle of projection θ at the time of projection vertically upward electric field E is switched on. When it reaches the maximum height electric filed is switched off and a horizontal electric feild of same magnitude E is switched on. Then answer the following question (Assume mg> qE)
Q If the time of flight to the maximum height is t1 and the time of flight maximum height to the ground is t2 thenView SolutionA pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate

a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.View SolutionA charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one pint. If a magnetic field is switched on in the vertical direction, the tension in the string
View SolutionA beam of electrons passes undeflected through uniformly perpendicular electric and magnetic fields. If the electric field is switched off, and the same magnetic field is maintained then the electrons move:
View SolutionA ball having charge q and mass m is suspended from a string of length L between two parallel plates where a vertical electric field E is established . Find the time period of simple pendulum if electric field is directed (a) downward and (b) upward.
View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then
 View Solution
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then
 View Solution
View Solution

