Electric field at centre of quarter circular ring having charge density λ is _____
√2λ4πε0r
λ2πε0r
λε0r
√2λ2πε0r
The correct Answer is:A
To find the electric field at the center of a quarter circular ring with a linear charge density λ, we can follow these steps:
Step 1: Understand the Geometry
We have a quarter circular ring of radius r in the xy-plane, centered at the origin. The charge density is given as λ.
Step 2: Consider a Small Element of Charge
Let’s consider a small segment of the ring, dq, which subtends an angle dθ at the center. The length of this small segment is rdθ.
Step 3: Express the Charge Element
The charge dq can be expressed in terms of the linear charge density:
dq=λ⋅(rdθ)
Step 4: Calculate the Electric Field Contribution
The electric field dE due to the charge element dq at the center of the ring is given by Coulomb's law:
dE=kdqr2
Substituting dq:
dE=kλ(rdθ)r2=kλrdθ
Step 5: Determine the Direction of the Electric Field
The electric field dE has both x and y components. The angle θ gives the direction:
- The x-component is dEx=dEcos(θ)
- The y-component is dEy=dEsin(θ)
Thus, we can write:
dEx=kλrcos(θ)dθ
dEy=kλrsin(θ)dθ
Step 6: Integrate to Find Total Electric Field
To find the total electric field E, we integrate dEx and dEy from 0 to π2:
Ex=∫π20dEx=∫π20kλrcos(θ)dθ
Ey=∫π20dEy=∫π20kλrsin(θ)dθ
Step 7: Evaluate the Integrals
The integrals evaluate to:
Ex=kλr(sin(θ))π20=kλr(1−0)=kλr
Ey=kλr(−cos(θ))π20=kλr(0−(−1))=kλr
Step 8: Combine the Components
The total electric field E at the center is:
E=Ex^i+Ey^j=kλr^i+kλr^j
This can be expressed as:
E=kλr(^i+^j)
Step 9: Calculate the Magnitude
The magnitude of the electric field is:
|E|=kλr√12+12=kλr√2
Step 10: Substitute k
Using k=14πϵ0:
|E|=√2λ4πϵ0r
Final Answer
The electric field at the center of the quarter circular ring is:
E=√2λ4πϵ0r
We have a quarter circular ring of radius r in the xy-plane, centered at the origin. The charge density is given as λ.
Let’s consider a small segment of the ring, dq, which subtends an angle dθ at the center. The length of this small segment is rdθ.
The charge dq can be expressed in terms of the linear charge density:
dq=λ⋅(rdθ)
The electric field dE due to the charge element dq at the center of the ring is given by Coulomb's law:
dE=kdqr2
Substituting dq:
dE=kλ(rdθ)r2=kλrdθ
The electric field dE has both x and y components. The angle θ gives the direction:
- The x-component is dEx=dEcos(θ)
- The y-component is dEy=dEsin(θ)
dEx=kλrcos(θ)dθ
dEy=kλrsin(θ)dθ
To find the total electric field E, we integrate dEx and dEy from 0 to π2:
Ex=∫π20dEx=∫π20kλrcos(θ)dθ
Ey=∫π20dEy=∫π20kλrsin(θ)dθ
The integrals evaluate to:
Ex=kλr(sin(θ))π20=kλr(1−0)=kλr
Ey=kλr(−cos(θ))π20=kλr(0−(−1))=kλr
The total electric field E at the center is:
E=Ex^i+Ey^j=kλr^i+kλr^j
This can be expressed as:
E=kλr(^i+^j)
The magnitude of the electric field is:
|E|=kλr√12+12=kλr√2
Using k=14πϵ0:
|E|=√2λ4πϵ0r
The electric field at the center of the quarter circular ring is:
E=√2λ4πϵ0r
Topper's Solved these Questions
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE - II INTENSITY OF ELECTRIC FIELD) (LEVEL - II (MAIN) STRAIGHT OBJECTIVE TYPE QUESTION)
Explore 10 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE - II INTENSITY OF ELECTRIC FIELD) (LEVEL - II (MAIN) MORE THAN ONE ANSWER TYPE QUESTION)
Explore 1 Video
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE - I COULOMB.S INVERSE SQUARE LAQW) (LEVEL - II (ADVANCED LINKED COMPREHENSION TYPE QUESTION)
Explore 3 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:ADDITIONAL EXERCISE
Explore 13 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 10 Videos
Similar Questions
Electric field at centre O of semicircule of radius 'a' having linear charge density λ given is given by

View SolutionFind the electric field at centre of semicircular ring shown in figure .
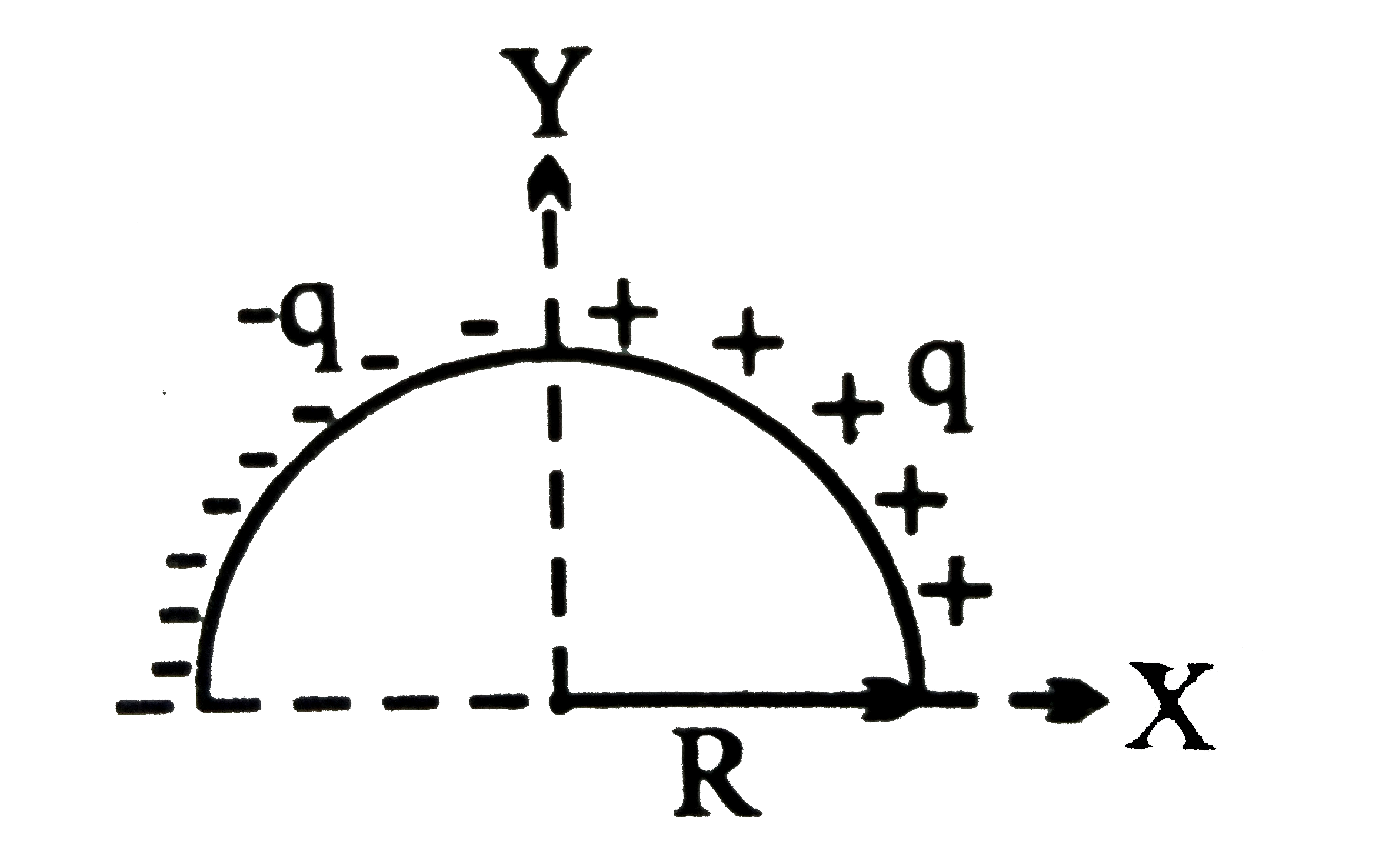 .
.
View SolutionFind the electric field at point O, due to the segment of a ring, whose linear charge density is 8C/cm

View SolutionElectric field at centre of a uniforly charged semicirlce of radius a is
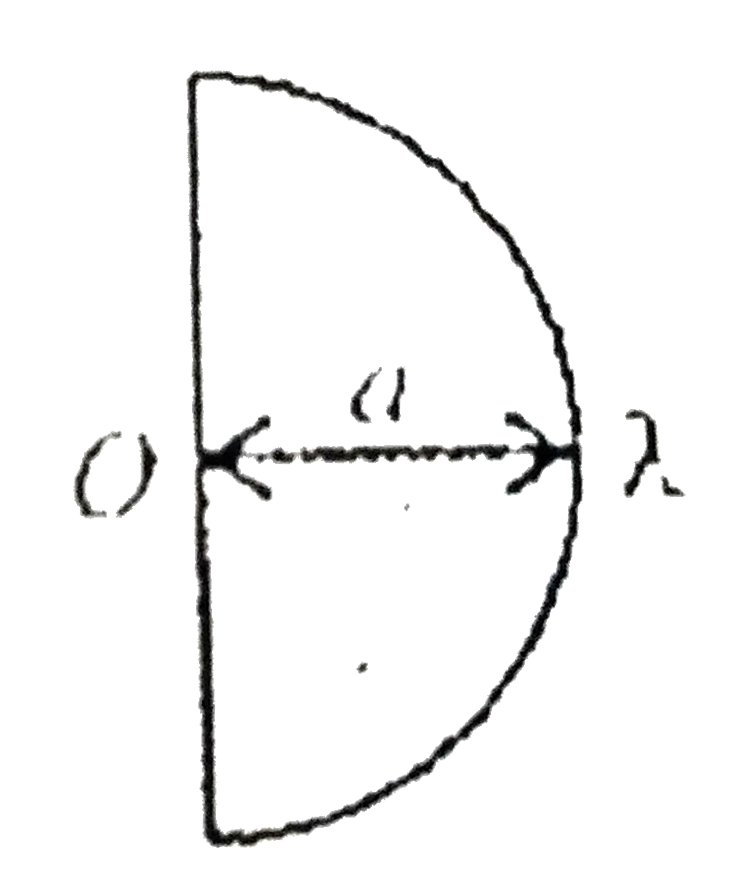
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionCalculate magnetic flux density of the magnetic field at the centre of a circular coil of 50 turns, having radius of 0.5 m and carrying a current of 5A.
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View Solution
