A student performs meter bridge experiment to determine specific resistance of a conducting wire of length 10cm and diameter 1mm. When a standard 6Ω resistance is connected on left gap and the given conducting wire is connected on the right gap, the balance points obtained for 60cm length of the meter bridge wire. The specific resistance in Ω−m for material of the given wire is:
3.14×10−2
6.28×10−2
3.14×10−5
6.28×10−5
The correct Answer is:C
To determine the specific resistance (ρ) of a conducting wire using the meter bridge experiment, we can follow these steps:
1. Understanding the Setup:
- We have a meter bridge where a standard 6 Ω resistance is connected on the left gap and a conducting wire of length 10 cm and diameter 1 mm is connected on the right gap.
- The balance point is obtained at 60 cm on the meter bridge.
2. Using the Meter Bridge Formula:
- The balance condition of the meter bridge is given by the formula:
R1R=L1L
- Where:
- R1 is the resistance on the left (6 Ω),
- R is the resistance of the wire,
- L1 is the length of the bridge wire on the left (60 cm),
- L is the total length of the bridge wire (100 cm).
3. Calculating the Resistance of the Wire:
- From the balance condition, we can rearrange the formula to find R:
R=LL1×R1
- Substituting the values:
R=100cm60cm×6Ω=10060×6=106×6=10Ω
4. Finding the Specific Resistance:
- The resistance of a wire is given by the formula:
R=ρLA
- Where:
- ρ is the specific resistance,
- L is the length of the wire (10 cm = 0.1 m),
- A is the cross-sectional area of the wire.
- The cross-sectional area A for a wire with diameter d is calculated as:
A=πd24
- Given that the diameter d=1mm=1×10−3m:
A=π(1×10−3)24=π×10−64=3.14×10−64≈7.85×10−7m2
5. Substituting Values to Find ρ:
- Rearranging the resistance formula to find ρ:
ρ=RAL
- Substituting the known values:
ρ=10Ω×7.85×10−7m20.1m=10×7.85×10−6Ω⋅m=7.85×10−5Ω⋅m
6. Final Result:
- The specific resistance of the material of the given wire is approximately:
ρ≈7.85×10−5Ω⋅m
- We have a meter bridge where a standard 6 Ω resistance is connected on the left gap and a conducting wire of length 10 cm and diameter 1 mm is connected on the right gap.
- The balance point is obtained at 60 cm on the meter bridge.
- The balance condition of the meter bridge is given by the formula:
R1R=L1L
- Where:
- R1 is the resistance on the left (6 Ω),
- R is the resistance of the wire,
- L1 is the length of the bridge wire on the left (60 cm),
- L is the total length of the bridge wire (100 cm).
- From the balance condition, we can rearrange the formula to find R:
R=LL1×R1
- Substituting the values:
R=100cm60cm×6Ω=10060×6=106×6=10Ω
- The resistance of a wire is given by the formula:
R=ρLA
- Where:
- ρ is the specific resistance,
- L is the length of the wire (10 cm = 0.1 m),
- A is the cross-sectional area of the wire.
- The cross-sectional area A for a wire with diameter d is calculated as:
A=πd24
- Given that the diameter d=1mm=1×10−3m:
A=π(1×10−3)24=π×10−64=3.14×10−64≈7.85×10−7m2
- Rearranging the resistance formula to find ρ:
ρ=RAL
- Substituting the known values:
ρ=10Ω×7.85×10−7m20.1m=10×7.85×10−6Ω⋅m=7.85×10−5Ω⋅m
- The specific resistance of the material of the given wire is approximately:
ρ≈7.85×10−5Ω⋅m
Topper's Solved these Questions
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Straight Objective Type Questions
19 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - Exercise -I
10 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
60 Videos
Similar Questions
In a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
A wire of length 1 m and radius 0.1mm has a resistance of 100(Ω).Find the resistivity of the material .
View SolutionWhen a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionIn metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is '1'. If the temperature of water is increased, the new balancing
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
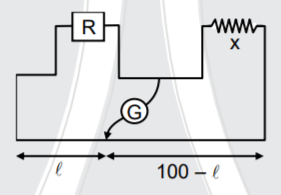
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is

View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View Solution
