In metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is '1'. If the temperature of water is increased, the new balancing
<l
>l
=0
=l
The correct Answer is:B
To solve the problem regarding the meter bridge experiment, we will follow these steps:
Step 1: Understand the Initial Setup
In the meter bridge experiment, we have a standard resistance R on one side (right gap) and a resistance coil X dipped in water on the other side (left gap). The initial balancing length obtained is L.
Step 2: Apply the Principle of the Meter Bridge
According to the principle of the meter bridge (which is based on the Wheatstone bridge principle), the balancing condition is given by:
XR=L100−L
Here, L is the length of the bridge corresponding to the resistance X, and 100−L corresponds to the resistance R.
Step 3: Consider the Effect of Temperature on Resistance
When the temperature of the water increases, the resistance X of the coil will also increase. This is because the resistance of conductors typically increases with temperature. We denote the new resistance as X′, where X′>X.
Step 4: Write the New Balancing Condition
With the new resistance X′, the new balancing length L′ can be expressed as:
X′R=L′100−L′
Since X′>X, the ratio X′R will also be greater than the original ratio XR.
Step 5: Analyze the Implications of the Increased Resistance
Given that X′R>XR, it follows that:
L′100−L′>L100−L
This indicates that the new balancing length L′ must be greater than the original balancing length L.
Conclusion
Thus, when the temperature of the water is increased, the new balancing length L′ will be greater than the original balancing length L.
Final Answer
The new balancing length L′ will be greater than L.
In the meter bridge experiment, we have a standard resistance R on one side (right gap) and a resistance coil X dipped in water on the other side (left gap). The initial balancing length obtained is L.
According to the principle of the meter bridge (which is based on the Wheatstone bridge principle), the balancing condition is given by:
XR=L100−L
Here, L is the length of the bridge corresponding to the resistance X, and 100−L corresponds to the resistance R.
When the temperature of the water increases, the resistance X of the coil will also increase. This is because the resistance of conductors typically increases with temperature. We denote the new resistance as X′, where X′>X.
With the new resistance X′, the new balancing length L′ can be expressed as:
X′R=L′100−L′
Since X′>X, the ratio X′R will also be greater than the original ratio XR.
Given that X′R>XR, it follows that:
L′100−L′>L100−L
This indicates that the new balancing length L′ must be greater than the original balancing length L.
Thus, when the temperature of the water is increased, the new balancing length L′ will be greater than the original balancing length L.
The new balancing length L′ will be greater than L.
Similar Questions
In a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionWhen a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
In a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
View SolutionA student performs meter bridge experiment to determine specific resistance of a conducting wire of length 10cm and diameter 1mm. When a standard 6Ω resistance is connected on left gap and the given conducting wire is connected on the right gap, the balance points obtained for 60cm length of the meter bridge wire. The specific resistance in Ω−m for material of the given wire is:
View SolutionDetermination of unknonw resistance in metre bridge is most accurate , when the balancing length is
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
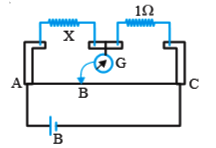
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
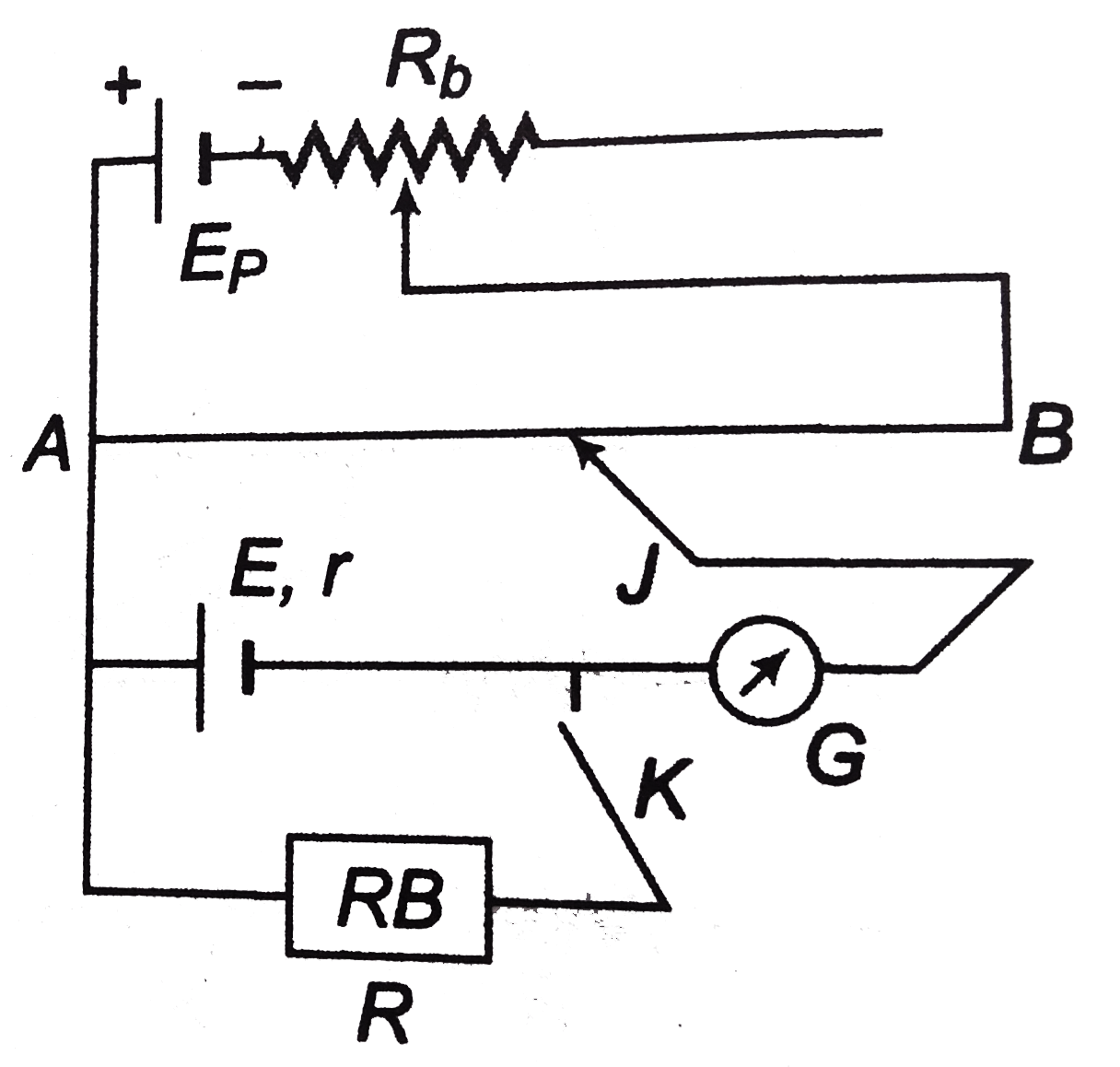
View SolutionIn an experiment on the measurement of internal resistance of as cell by using a potentionmeter, when the key K is kept open then balancing length is obtained at y metre. When the key K is closed and some resistance R is inserted in the resistance box, then the balancing length is found to be x metre. Then the internal resistance is
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
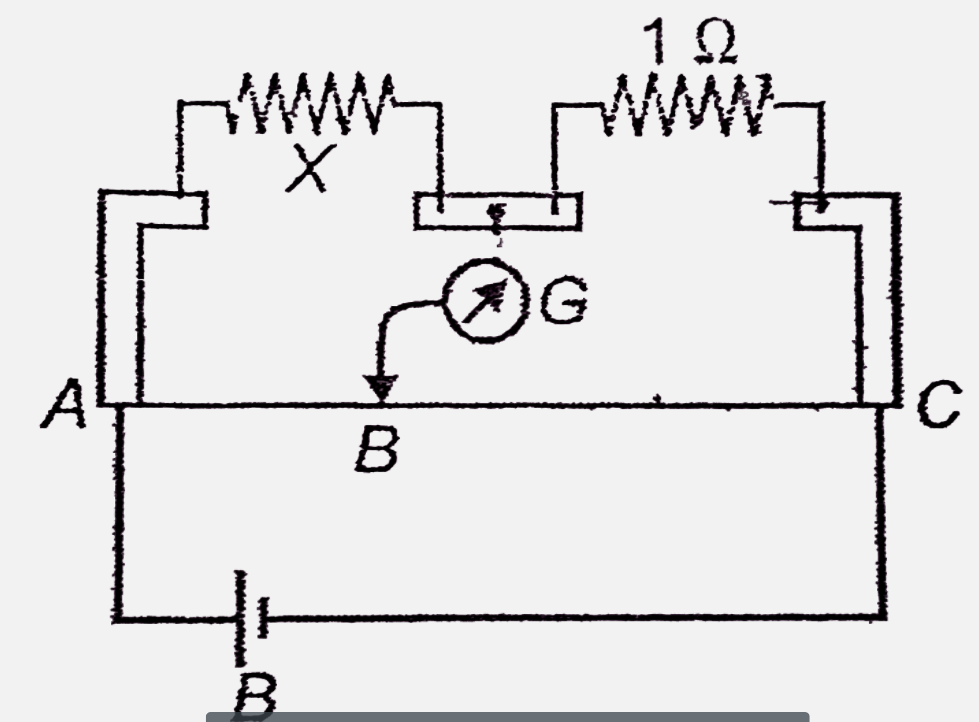
View Solution
