In remeasurement of mass of a given object by the principle of moments, the meter scale is hung from its midd -point. A known weight of mass 2kg is hung at one end of meter scale at distance 50 cm and unknown weight of mass m kg is bung at 20cm from the centre on other side. The Value of m is
2kg
5kg
2.5 kg
0.8 kg
The correct Answer is:B
To solve the problem of finding the unknown mass m using the principle of moments, we can follow these steps:
1. Understand the Setup:
- A meter scale is hung from its midpoint.
- A known mass of 2kg is hung at one end (50 cm from the center).
- An unknown mass m is hung at a distance of 20cm from the center on the other side.
2. Identify the Forces:
- The weight of the known mass 2kg is W1=2g (where g is the acceleration due to gravity).
- The weight of the unknown mass m is W2=mg.
3. Apply the Principle of Moments:
- For the system to be in equilibrium (balanced), the clockwise moments about the pivot point must equal the counterclockwise moments.
- The moment due to the known mass is given by:
Moment1=W1×Distance from center=(2g)×0.5m=2g×0.5=g
- The moment due to the unknown mass is given by:
Moment2=W2×Distance from center=(mg)×0.2m=mg×0.2
4. Set the Moments Equal:
- Since the scale is balanced, we can set the two moments equal to each other:
g=mg×0.2
5. Cancel g from Both Sides:
- Assuming g≠0, we can divide both sides by g:
1=m×0.2
6. Solve for m:
- Rearranging the equation gives:
m=10.2=5kg
Final Answer:
The value of the unknown mass m is 5kg.
---
- A meter scale is hung from its midpoint.
- A known mass of 2kg is hung at one end (50 cm from the center).
- An unknown mass m is hung at a distance of 20cm from the center on the other side.
- The weight of the known mass 2kg is W1=2g (where g is the acceleration due to gravity).
- The weight of the unknown mass m is W2=mg.
- For the system to be in equilibrium (balanced), the clockwise moments about the pivot point must equal the counterclockwise moments.
- The moment due to the known mass is given by:
Moment1=W1×Distance from center=(2g)×0.5m=2g×0.5=g
- The moment due to the unknown mass is given by:
Moment2=W2×Distance from center=(mg)×0.2m=mg×0.2
- Since the scale is balanced, we can set the two moments equal to each other:
g=mg×0.2
- Assuming g≠0, we can divide both sides by g:
1=m×0.2
- Rearranging the equation gives:
m=10.2=5kg
The value of the unknown mass m is 5kg.
Topper's Solved these Questions
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - Exercise -I
10 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
60 Videos
Similar Questions
Two points objects of mass 1.5g and 2.5g respectively are a distance of 16cm apart, the center of mass is at distance x from the object of mass 1.5g. Find the value of x
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
View Solution
Knowledge Check
A uniform rod of length 1m mass 4kg is supports on tow knife-edges placed10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
Aa. 60 N, 40 NBb. 75 N, 25 NCc. 65 N, 35 NDd. 55 N, 45 N
A uniform meter scale of mass 1kg is placed on table such that a part of the scale is beyond the edge. If a body of mass 0.25kg is hung at the end of the scale then the minimum length of scale that should lie on the table so that it does not tilt is
View SolutionTwo painters are working from a wooden hoard 5m long suspended from the top of a building by two ropes attached to the ends of the plank. Either rope can withstand a maximum tension of 1040N. Painter A of mass 80kg is working at a distance of 1m from one end. Painter B of mass 60kg is working at a distance of x in from the centre of mass of the board on the other side. Take mass of the board as 20kg and g=10ms−2. The range of x so that both the painters can work safely is
View SolutionOn earth the weight of a body of mass 1.0 kg is 10 N. What will be the weight of a boy of mass 37 kg in kgf
View SolutionA uniform meter scale is kept in equilibrium when supported at the 60 cm mark and a mass weight of the scale is greater than, less than or equal to the weight of mass M.
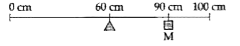
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle and other particle of mass 2kg is placed on centroid of triangle which is at a distance of √2 m from each of the vertices of the triangle .The force in newton , acting on the particle of mass 2 kg is
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Draw a diagram of the arrangement.
View SolutionCalcualte the intensily of gravitational field due to a body of mass 20kg at a distance of 50cm from the body ?
View Solution
