In an experiment with potentiometer to measure the internal resistance of a cell, when the cell is shunted by 5Ω, the null point is obtained at 2m. when cell is shunted by 20Ω the null point is obtained at 3m.The internal resistance of cell is
2Ω
4Ω
6Ω
8Ω
The correct Answer is:B
To solve the problem of finding the internal resistance of the cell using the potentiometer method, we will follow these steps:
1. Define Variables:
- Let E be the emf of the cell.
- Let r be the internal resistance of the cell.
- Let k be the potential gradient of the potentiometer wire.
2. Set Up the First Condition (5 Ω Shunt):
- When the cell is shunted by 5Ω, the null point is obtained at 2m.
- According to the potentiometer principle, we can write:
Er+5×5=k×2
- Rearranging gives:
Er+5=2k5(Equation 1)
3. Set Up the Second Condition (20 Ω Shunt):
- When the cell is shunted by 20Ω, the null point is obtained at 3m.
- Similarly, we can write:
Er+20×20=k×3
- Rearranging gives:
Er+20=3k20(Equation 2)
4. Equate the Two Conditions:
- From Equation 1 and Equation 2, we can equate:
Er+5⋅203=Er+20⋅52
- This simplifies to:
r+20r+5=23⋅205
- Simplifying further gives:
r+20r+5=83
5. Cross-Multiply and Solve for r:
- Cross-multiplying gives:
3(r+20)=8(r+5)
- Expanding both sides:
3r+60=8r+40
- Rearranging gives:
60−40=8r−3r
- Thus:
5r=20⇒r=4Ω
6. Conclusion:
- The internal resistance of the cell is r=4Ω.
- Let E be the emf of the cell.
- Let r be the internal resistance of the cell.
- Let k be the potential gradient of the potentiometer wire.
- When the cell is shunted by 5Ω, the null point is obtained at 2m.
- According to the potentiometer principle, we can write:
Er+5×5=k×2
- Rearranging gives:
Er+5=2k5(Equation 1)
- When the cell is shunted by 20Ω, the null point is obtained at 3m.
- Similarly, we can write:
Er+20×20=k×3
- Rearranging gives:
Er+20=3k20(Equation 2)
- From Equation 1 and Equation 2, we can equate:
Er+5⋅203=Er+20⋅52
- This simplifies to:
r+20r+5=23⋅205
- Simplifying further gives:
r+20r+5=83
- Cross-multiplying gives:
3(r+20)=8(r+5)
- Expanding both sides:
3r+60=8r+40
- Rearranging gives:
60−40=8r−3r
- Thus:
5r=20⇒r=4Ω
- The internal resistance of the cell is r=4Ω.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )143videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
In an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionA Daniel cell is balanced on 125cm length of a potentiometer wire. Now the cells is short-circuited by a resistance 2ohm and the balance is obtained at 100cm. The internal resistance of the Dainel cell is
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionIn the metrebridge experiment , the null point is obtained at N. The value of unkonw resistance X will be .
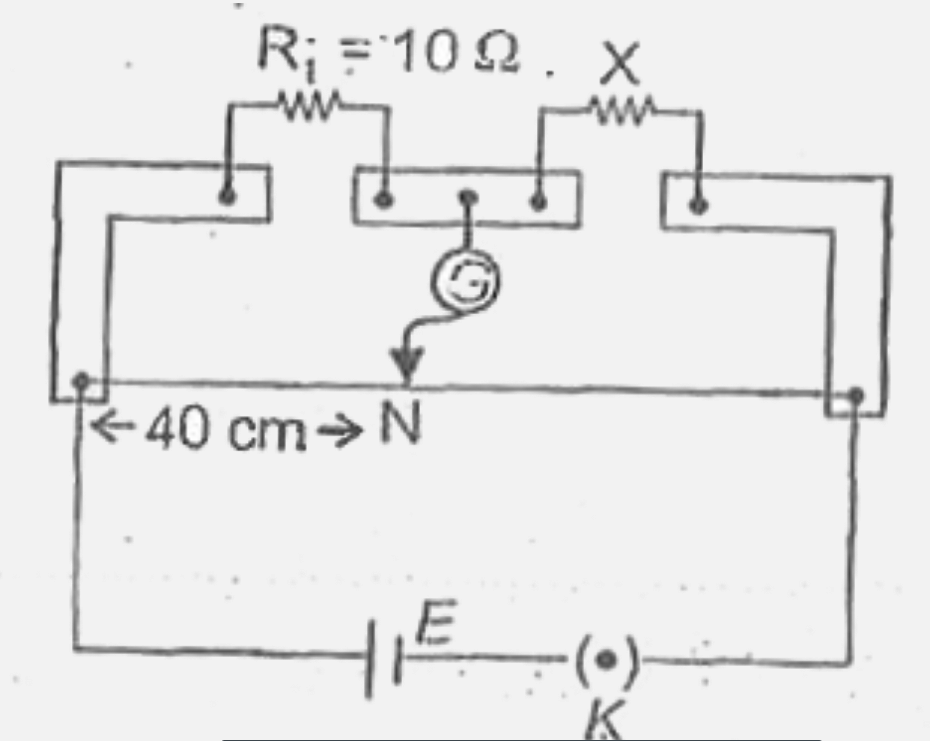 View Solution
View SolutionIn a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionFor the given circuit,
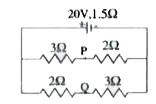
If internal resistance of cell is 1.5Ω, thenView SolutionFor a cell, the terminal potential difference is 2.2V, when circuit is open and reduces to 1.8V. When cell is connected to a resistance R=5Ω, the internal resistance of cell (R) is
View Solution

