A potentiometer wire of 5m length and having 20Ωresistance is connected in series with a battery and a resistance of 3980Ω. A cell of emf 1.1V is balanced across the potential difference of the external resistance. If the emf of the thermocouple is 2.2mV, the corresponding balancing length is
398cm
200cm
450cm
306cm
The correct Answer is:B
To solve the problem step by step, we will follow the outlined procedure:
Step 1: Identify Given Values
- Length of the potentiometer wire (L) = 5 m
- Resistance of the potentiometer wire (R_wire) = 20 Ω
- External resistance (R_ext) = 3980 Ω
- EMF of the cell (E_cell) = 1.1 V
- EMF of the thermocouple (E_thermocouple) = 2.2 mV = 2.2 × 10^(-3) V
Step 2: Calculate Total Resistance
The total resistance in the circuit (R_total) is the sum of the resistance of the potentiometer wire and the external resistance:
Rtotal=Rwire+Rext=20Ω+3980Ω=4000Ω
Step 3: Calculate the Current (I)
Using Ohm's Law, the current (I) flowing through the circuit can be calculated as:
I=EcellRtotal
Substituting the values:
I=1.1V4000Ω=0.000275A=2.75mA
Step 4: Calculate the Potential Gradient (K)
The potential gradient (K) is given by the formula:
K=I⋅RwireL
Substituting the values:
K=(0.000275A)⋅(20Ω)5m
K=0.0055V5m=0.0011V/m=1.1mV/m
Step 5: Calculate the Balancing Length (L_bal)
The balancing length (L_bal) can be calculated using the formula:
Lbal=EthermocoupleK
Substituting the values:
Lbal=2.2×10−3V1.1×10−3V/m=2m
Step 6: Convert to Centimeters
Since the problem asks for the balancing length in centimeters:
Lbal=2m×100=200cm
Final Answer
The corresponding balancing length is 200 cm.
---
- Length of the potentiometer wire (L) = 5 m
- Resistance of the potentiometer wire (R_wire) = 20 Ω
- External resistance (R_ext) = 3980 Ω
- EMF of the cell (E_cell) = 1.1 V
- EMF of the thermocouple (E_thermocouple) = 2.2 mV = 2.2 × 10^(-3) V
The total resistance in the circuit (R_total) is the sum of the resistance of the potentiometer wire and the external resistance:
Rtotal=Rwire+Rext=20Ω+3980Ω=4000Ω
Using Ohm's Law, the current (I) flowing through the circuit can be calculated as:
I=EcellRtotal
Substituting the values:
I=1.1V4000Ω=0.000275A=2.75mA
The potential gradient (K) is given by the formula:
K=I⋅RwireL
Substituting the values:
K=(0.000275A)⋅(20Ω)5m
K=0.0055V5m=0.0011V/m=1.1mV/m
The balancing length (L_bal) can be calculated using the formula:
Lbal=EthermocoupleK
Substituting the values:
Lbal=2.2×10−3V1.1×10−3V/m=2m
Since the problem asks for the balancing length in centimeters:
Lbal=2m×100=200cm
The corresponding balancing length is 200 cm.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
A potentiometer wire of length 1m and resistance 20Ω is connected in series with a 15V battery and an external resistance 40Ω . A secondary cell of emf E in the secondary circuit is balanced by 24 cm long potentiometer wire. The emf E of the cell is ,
View SolutionA potentiometer wire of Length L and a resistance r are connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire. The e.m.f. E will be given by :
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
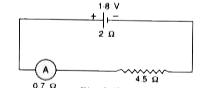
View SolutionA cell which has an emf 1.5 V is connectedin series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
View SolutionA potentiometer wire has length 4m and resistance 8Ω. The resistance that must be connected in series with the wire and an accumulator of e.m.f. 2V, so as the get a potential gradient 1mV per cm on the wire is
View SolutionA potentiometer wire has length 4m and resistance 8Ω. The resistance that must be connected in series with the wire and an accumulator of e.m.f. 2V, so as the get a potential gradient 1mV per cm on the wire is
View SolutionA potentiometer wire of length 10m and resistance 30 ohm is connected in series with a battery of emf 2.5V, internal resistance 5 ohm and external resistance R. If the fall of potential along the potentiometer wire is 50mV/m, the value of R is ohms is
View SolutionA potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionA potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View Solution
