A concrete bridge is designed as a parabolic arch. The road over bridge is 40m long and the maximum height of the arch is 15m . Write the equation of the parabolic arch.
The correct Answer is:80 y
Topper's Solved these Questions
- TWO DIMENSIONAL ANALYTICAL GEOMETRY-IIBook:NCERT TAMILChapter:TWO DIMENSIONAL ANALYTICAL GEOMETRY-IIExercise:EXERCISE 5.1
Explore 14 Videos
- TWO DIMENSIONAL ANALYTICAL GEOMETRY-IIBook:NCERT TAMILChapter:TWO DIMENSIONAL ANALYTICAL GEOMETRY-IIExercise:EXERCISE 5.2
Explore 11 Videos
- THEORY OF EQUATIONS Book:NCERT TAMILChapter:THEORY OF EQUATIONS Exercise:EXERCISE 3.7
Explore 10 Videos
- VECTOR ALGEBRABook:NCERT TAMILChapter:VECTOR ALGEBRAExercise:Miscellaneous Exercise on chapter 10
Explore 19 Videos
Similar Questions

The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The equation of the parabola designed on the bridge can be
View Solution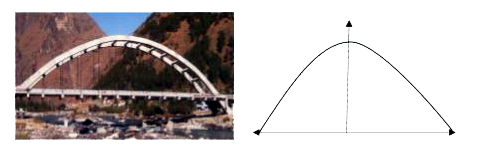
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The integrand of the integral ∫50−50x2dx is ________ function.
View Solution
Knowledge Check
In a model, it is shown that an arc of a bridge in semi-elliptical with major axis horizontal. If the length of the base is 9 m and the highest part of the bridge is 3 m from the horizontal, the best approximation of the height of the arch at 2 m from the centre of the base is
A11/4 mB8/3 mC7/2 mD2 mAn arc of a bridge is semi-elliptical with major axis horizontal. If the length of the base is 9 m and highest part of the bridge is 3 m from the base, then what will be the best approximation of the height of the arch 2 m from the centre of the base?
A114mB83mC72mD2m

The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The value of the integral ∫50−50x2250dx is
View Solution
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The area formed by the curve x2=250y, x-axis , y = 0 and y = 10 is
View Solution
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The area formed between x2=250y, y-axis , y = 2 and y = 4 is
View SolutionIF the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionIf the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionIn a model, it is shown that an arc of a bridge is semi elliptical with major axis horizontal. If the length of the base is 9m and the highest part of the bridge is 3m from the horizontal, then the height of the arch, 2m from the centre of the base is (in meters)
View Solution
