Th e velocity of a particle moving in a plane is given by the following diagram. Find out the direction of force acting on the particle?

The velocity of the particle is →v=→jxˆi+vyˆj+v2ˆk. As shown in the fi gure, the particle is moving in the xy plane, there is no motion in the z direction. So velocity in the z direction is zero (vz=0). The velocity of the particle has x component (vx) and y component (vy). From fi gure, as time increases from t = 0 sec to t = 3 sec, the length of the vector in y direction is changing (increasing). It means y component of velocity (vy) is increasing with respect to time. According to Newton’s second law, if velocity changes with respect to time then there must be acceleration. In this case, the particle has acceleration in the y direction since the y component of velocity changes. So the particle experiences force in the y direction. Th e length of the vector in x direction does not change. It means that the particle has constant velocity in the x direction. So no force or zero net force acts in the x direction
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT TAMILCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE ( I. Multiple Choice Questions)
15 Videos
- LAWS OF MOTIONBOOK - NCERT TAMILCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE (V. Numerical Problems)
14 Videos
- LAW OF MOTIONBOOK - NCERT TAMILCHAPTER - LAW OF MOTIONEXERCISE - EXERCISE (ADDITIONAL EXERCISE)
17 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - NCERT TAMILCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE
45 Videos
Similar Questions
Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.
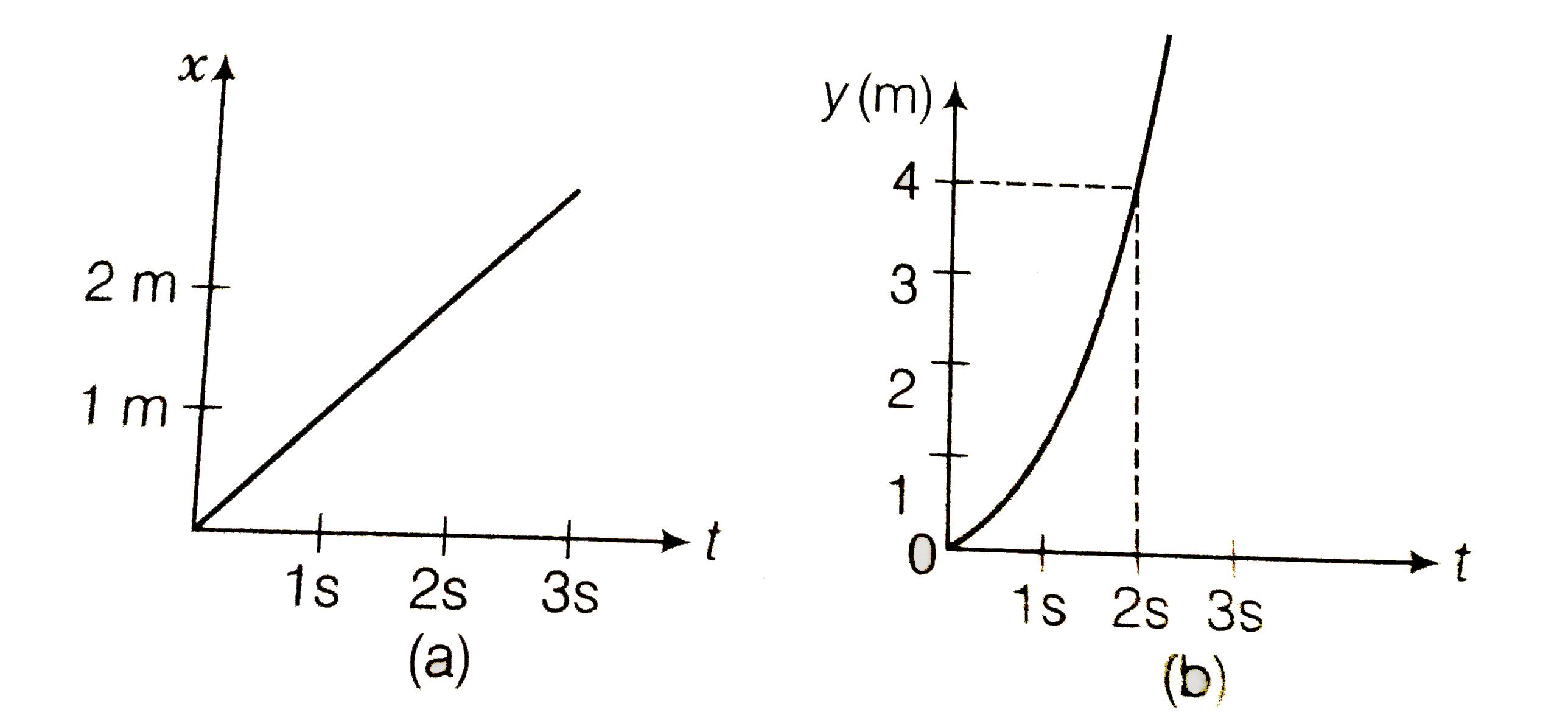
If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .
View SolutionThe velocity of a particle of mass 2 kg is given by →v=atˆi+bt2ˆj. Find the force acting on the particle.
View Solution
Knowledge Check
The K.E (K ) of a particle moving along a circle r depends upon the distance covered (s) as K=as2 The centripetal force acting on the particle is given by
A2asB2as2C2as2rD2ars2Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.

If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .A1N along y-axisB1N along x-axisC0.5N along x-axisD0.5N along y-axisA particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :
 AIncreaseBDecreaseCRemain constantDChange according to the smallest force
AIncreaseBDecreaseCRemain constantDChange according to the smallest force
Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.

If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .
View SolutionFigure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.

If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .
View SolutionFigure 3.E2 shows the velocity -time graph for a particle moving in a fixed direction. Find the acceleration of the particle.
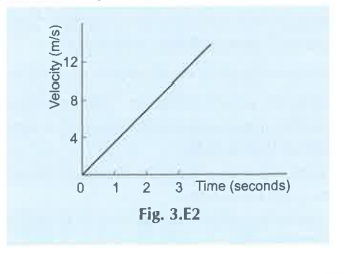
View SolutionA charged is moving with constant velocity parallel to a horizontal current carrying long wire. The direction of velocity of that particle and the current are same. If the force acting on the particle are only magnetic force due to wire and gravitational force due to earth, then the particle :
View SolutionA charged is moving with constant velocity parallel to a horizontal current carrying long wire. The direction of velocity of that particle and the current are same. If the force acting on the particle are only magnetic force due to wire and gravitational force due to earth, then the particle :
View Solution
