Locate the center of mass of a uniform rod of mass M and length A.

Text Solution

Verified by Experts

Consider a uniform rod of mass M and length A whose one end coincides with the origin as shown in Figure. The rod is kept along the x axis. To find the center of mass

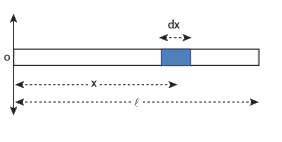
of this rod, we choose an infinitesimally small mass dm of elemental length dx at a distance x from the origin.
$λ$ is the linear mass density (i.e. mass per unit length) of the rod. $λ = \frac{M}{l}$
The mass of small element (dm) is, dm $= \frac{M}{l} d x$
Now, we can write the center of mass equation for this mass distribution as,
$x_{C M} = \frac{\int x d m}{\int d m}$
$x_{C M} = \frac{l \int o x (\frac{M}{l} d x)}{M} = \frac{1}{l} l \int o x d x$
$= \frac{1}{l} {[\frac{x^{2}}{2}]}_{0}^{1} = \frac{1}{l} (\frac{l^{2}}{2})$
$x_{C M} = \frac{l}{2}$
As the position $\frac{l}{2}$ is the geometric center of the rod, it is concluded that the center of mass of the uniform rod is located at its geometric center itself.

Updated on:21/07/2023