A particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium. Solution in Gujrati

The situation is shown in figure . Supppose the
piont suspension is O and let theta be the angle between
the thread and the vertical. Forces on the particle B are
(i) weight mg downward
(ii) tension T along the thread and
(iii) electric force of repulsion F along AB.
For equilibrium, these forces should add to zero. Let
X'' BX be the line perpendicular to OB. we shall take the
components of the forces along BX. This will giva a
relation between F, mg and θ
The verious andgles are shown in the figure. As
OA=OB,∠OAB= 90^@ - (theta)/(2)<br>Theother∠scanbewritendowndirectly.<br>Tak∈gcompo≠ntsalongBX,we≥t<br>F cos (theta) /(2) = mg cos ( 90^@ - theta)<br>= 2 mg sin (theta)/(2) cos (theta)/(2)<br>or,sin (theta)/(2) = (F)/ (2mg)<br>Now, F = (9xx10 ^9 Nm^2 C^(-2) xx (5.0 xx 10 ^(-7) C)^2 xx (1)/(AB^2)<br>andAB = 2 (OA) sin (theta)/(2).<br>Thus,F = (9 xx 10 ^9 xx 25 xx 10(-14))/(4 xx (30xx10^(-2))^2 xx sin^2. (theta)/(2)) N<br>om(i)and(ii),<br>sin (theta)/(2) = (F )/(2 mg) = (9xx 10^9 xx 25 xx 10 ^(-14) N )/(4xx ( 30 xx 10 ^(-2)^2 xx sin^2 .(theta)/(2)) . (1)/(2mg) or
sin3(θ)2=9×109×25×10−14N4×9×10−2×2×(100×10−3kg)×9.8ms(−2)
=0.0032
or sin (theta)/(2) = 0.15, giving theta =17^@.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Short Answer14videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 19videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises23videos
ELECTRIC CURRENT THROUGH GASES
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
Similar Questions
The charge on a proton is +1.6X10(−19)C and that on an electron is −1.6X10(−19)C. Does it mean that the electron has a charge 3.2X10(−19)C less than the charge of a proton?
03:49View SolutionFigure shows some of the electric field lines correspoinding to an electric field. The figure suggests that
 09:59View Solution
09:59View SolutionFind the dimensional formula of ε0 .
06:11View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
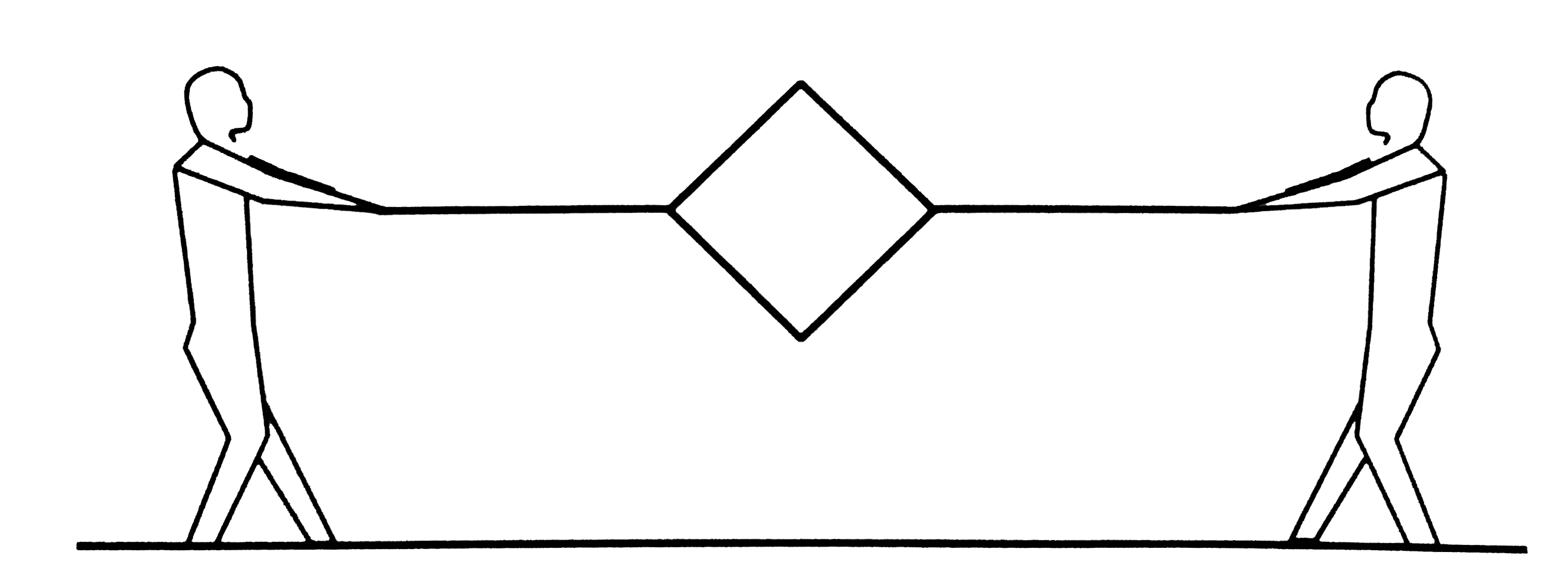
03:30View SolutionShown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
 05:44View Solution
05:44View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.View SolutionA particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium.
06:02View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a xharged nonconducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of 4.0×10C. In equilibrium, the thread make an angle of 600 with the vertical. Find the surface charge dendity on the plate.
11:16View SolutionBelow the fixed end O of the insulating horizontal thread OB, there is a fixed charge A of Q = 20muc . At the end B of the thread there is a small mass m carrying charge Q = 20moc . The mass is released from the position shown and it is found to come to rest when the thread becomes vertical. Assume that the thread does not hit the fixed charge at A. [g = 10 m//s^2] (a) Find mass m. (b) Find tension in the thread in the equilibrium position when the thread is vertical. (c) Is the equilibrium mentioned in (b) stable or unstable?
08:13View SolutionA particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge -q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30^(@) with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
13:15View SolutionA particle A having a charge of 5.0×10−7C is fixed in a vertical wall. A second particle B of mass 100g and having equal charge is suspended by a silk thread of length 30 cm from the wall. The point of suspension is located 30 cm vertically above the first particle. Find the angle of the thread with the vertical when it stays in equilibrium.
04:59View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.05:49View SolutionA particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium.
06:12View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non conducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of 4.0×10C. In equilibrium, the thread make an angle of 600 with the vertical. Find the surface charge density on the plate.
04:03View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and charge of 4×10−6C. In equilibrium, thread makes an angle of 60o with the vertical.
(a) Find the tension in the string in equilibrium.
(b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(Use σ=7.5×10−7Cm2)04:03View SolutionOne end of a 10 cm long skill thread is fixed to a large vertical surface of a charged nonconducting plate and the other end ise fastened to a small ball having a mass of 10 g and a charge of 4.0 xx 10^(-6)C . In equilibrium, the thread makes an angle of 60^(@) with the vertical. Find the tension in the string in equilibrium.
07:16View Solution

