A perfectly reflecting solid sphere of radius r is kept in the path of a parallel beam of light of large aperture. If the beam carries an intensity I, find the force exerted by the beam on the sphere. Solution in Gujrati

Let O be the centre of the sphere and OZ be the line
opposite to the incident beam. Consider
a radius OP of the sphere making an angle theta with OZ.
Rotate this radius about OZ to get a circle on the sphere.
Change theta to theta + d theta and rotate the radius about OZ to
get another circle on the sphere. The part of the sphere
between these circles is a ring of area (2π(r2)sinθdθ).
Consider a small part ΔA of this ring at P. Energy of
the light falling on this part in time (Δt) is
ΔU=I(Δt)(ΔAcosθ).
Themomentumofthislightfall∈gonΔAis(ΔUc)along<br>QP.Thelightisref≤ctedbythespherealongPR.The<br>chan≥∈momentumis<br> (Delta p = 2 (Delta U/ c ) cos theta = (2/c) I Delta t (Delta A (cos^2) theta)).<br>alongthe∈ward∥a∥l.Theforceon(ΔA)due→the<br>lightfall∈gonit,is<br> (Delta p/ Delta t ) = 2/c I (Delta A(cos^2)theta)<br>ThisforceisalongPO,therestant–––––forceonther∈g<br>aswellasonthesphereisalongZObysymmetry.The<br>compo≠ntoftheforceon Delta A,alongZOis.<br> (Delta p/ Delta t) cos theta = 2/c (I (Delta A)cos ^3) theta. <br> The force acting on the ring is ,
dF=(2c)I(2π(r2)(sinθ)dθ)cos3θ.
The force on the entire sphere is
F=(∫π20(4π(r2)Ic)(cos3)θsinθdthη)
=−(∫π2θ=0(4π(r2)Ic)cos3θd(cosθ).
=−(4π(r2)Ic)([cos4θ4]π20=(π(r2)Ic).
Note that integration is done only for the hemisphere
that faces the incident beam.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Short Answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Objective 1
14 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Worked Out Examples
4 Videos
- PERMANENT MAGNETSBOOK - HC VERMACHAPTER - PERMANENT MAGNETSEXERCISE - Exercises
25 Videos
- PHOTOMETRYBOOK - HC VERMACHAPTER - PHOTOMETRYEXERCISE - Exercises
16 Videos
Similar Questions
Can we find the mass of a photon by the definition p =mv?
View SolutionPlanck constant has the same dimensions as
View SolutionHow many photons are emitted per second by a 5m W laser source operating at 632.8nm?
View SolutionA long bar magnet has a pole strength of 10Am. Find the magnetic field at a point on the axis of the magnet at a distance of 5cm from the north pole of the magnet.
View SolutionA source emits 45 joules of energy in 15 s. What is the radiant flux of the source ?
View SolutionA perfectly reflecting solid sphere of radius r is kept in the path of a parallel beam of light of large aperture. If the beam carries an intensity I, find the force exerted by the beam on the sphere.
View SolutionA sphere of radius 1.00 cm is placed in the path of a parallel beam of light of large aperture. The intensity of the light is 0.50 W cm−2. If the sphere completely absorbs the radiation falling on it, find the force exerted by the light beam on the sphere.
View SolutionA parallel beam of light falls on a solid tranparent sphere. Q. Which is corret?
View SolutionA parallel beam of light falls on a solid tranparent sphere.
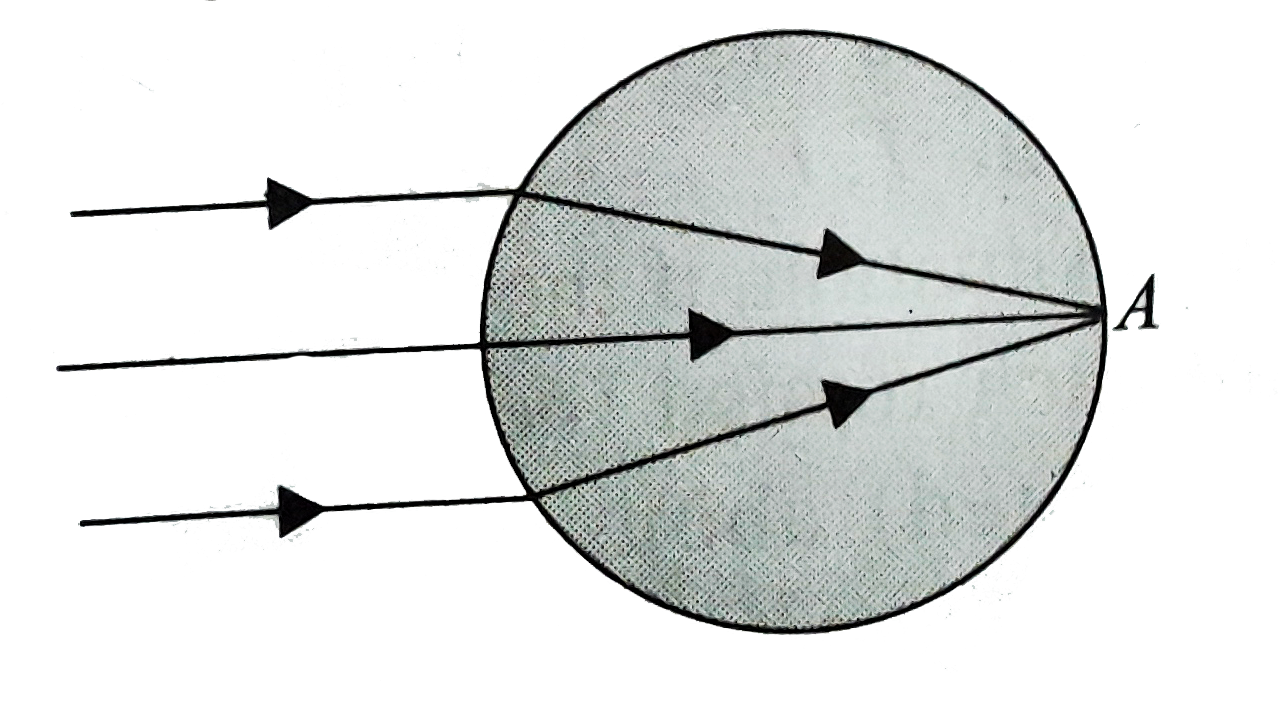
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionIn the path of a uniform light beam of large cross-sectional area and intensity I. a solid sphere of redius R which is perfectly reflecting is placed . Find the force exerted on this sphere due to the light beam.
View SolutionA parallel beam of monochromatic light of frequency v is incident on a surface. Intensity of the beam is I and area of the surface is A. Find the force exerted by the light beam on the surface for following cases–
(i) the surface is perfectly absorbing and the light beam is incident normally on it.
(ii) the surface is perfectly reflecting and the light beam is incident normally.
(iii) the surface is perfectly absorbing and the light beam is incident at an angle of incidence θ.
(iv) the surface is perfectly reflecting and the light beam is incident at an angle of incidence θ.
View SolutionFigure2.25 shows a cone of radius R and height H with perfectly reflecting lateral surface, is placed in the path of a light beam of intensity I. Find the force exerted on this cone.

View SolutionA perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
View SolutionA narror parallel beam of light is incident paraxially on a solid transparent sphere of radius r kept in air. What should be the refreative index if the beam is to be focusd (a) at the further surface of the sphere, (b) at the centre of the sphere.
View SolutionA parallel beam of monochromatic light of frequency v is indcident on a surface. The intensity of the beam is I and area of the surface is A. Find the force exerted by light of beam on the surface is perfectly reflecting and the light beam is incident at an angle of incidence θ. (The speed of light is denoted as c.)
View SolutionThere is a parallel beam of light of larger aperture . Let I be the intensity of light . Perfectly reflecting sphere of radius r is kept in the path of this parallel beam . Find the force exerted by the light beam on sphere .
View Solution
