A tap has water drops dripping from it at a steady rate of 3 drops per sec. What is the vertical separation (in metres) between two consecutive drops, at an instant when the lower drop has a velocity of 9m/s.
(take g=10m/s2)
The correct Answer is:2.44
Time taken by each drop to come out of tap=13S
At a given instant if drop A is in motion for
t1 s then drop B is in motion for (t1−13)s
For drop A,u=0,v=9m/s2,s=hA
a=10m/s2,t=t1
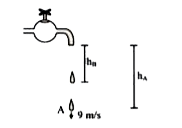
∴v=u+at
∴9=0+10×t1
∴R=71.42m
s=ut+12at2
∴ha=0+12×10×(0.9)2
∴ha=4.05m
For drop B,u=0,s=hB,a=10m/s2
t2=(t1−13)=0.9−13=1730s
s=ut+12at2
∴hB=0+12×10×(1730)2
∴hB≈1.61m
Vertical separation between drop A and B=hA=hB=−4.05−1.61=2.44m
Topper's Solved these Questions
Similar Questions
Water drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (takeg=10m−2)
View SolutionTwo balls are dropped simultaneously from two points separated by a vertical height of 6 m. The distance of separation between them after next 2s is
View Solution
Knowledge Check
Water drops fall at regular intervals from a roof. At an instant when a drop is about to leave the roof, the separations between 3 successive drops below the roof are in the ratio
A1:2:3B1:4:9C1:3:5D1:5:13Water drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (take=g=10m−2)
A1.25 mB2.15 mC2.75 mD3.75 mA stone is dropped from the top of tower. When it has fallen by 5m from the top, another stone is dropped from a point 25m below the top. If both stones reach the ground at the moment, then height of the tower from grounds is : (take g=10m/s2)
A45mB50mC60mD65m
A stone is dropped from the top of tower. When it has fallen by 5m from the top, another stone is dropped from a point 25m below the top. If both stones reach the ground at the moment, then height of the tower from grounds is : (take g=10m/s2)
View SolutionWater drops are falling from a tap in regular interval of time. A drop falls from the tap and after 4secs of falling the drop is 34.3m away from next drop. Then drops are falling at rate of ( g=9.8ms2)
View SolutionWater drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take g=9.8m/s2
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. (g=10ms−2)
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. (g=10ms−2)
View Solution
