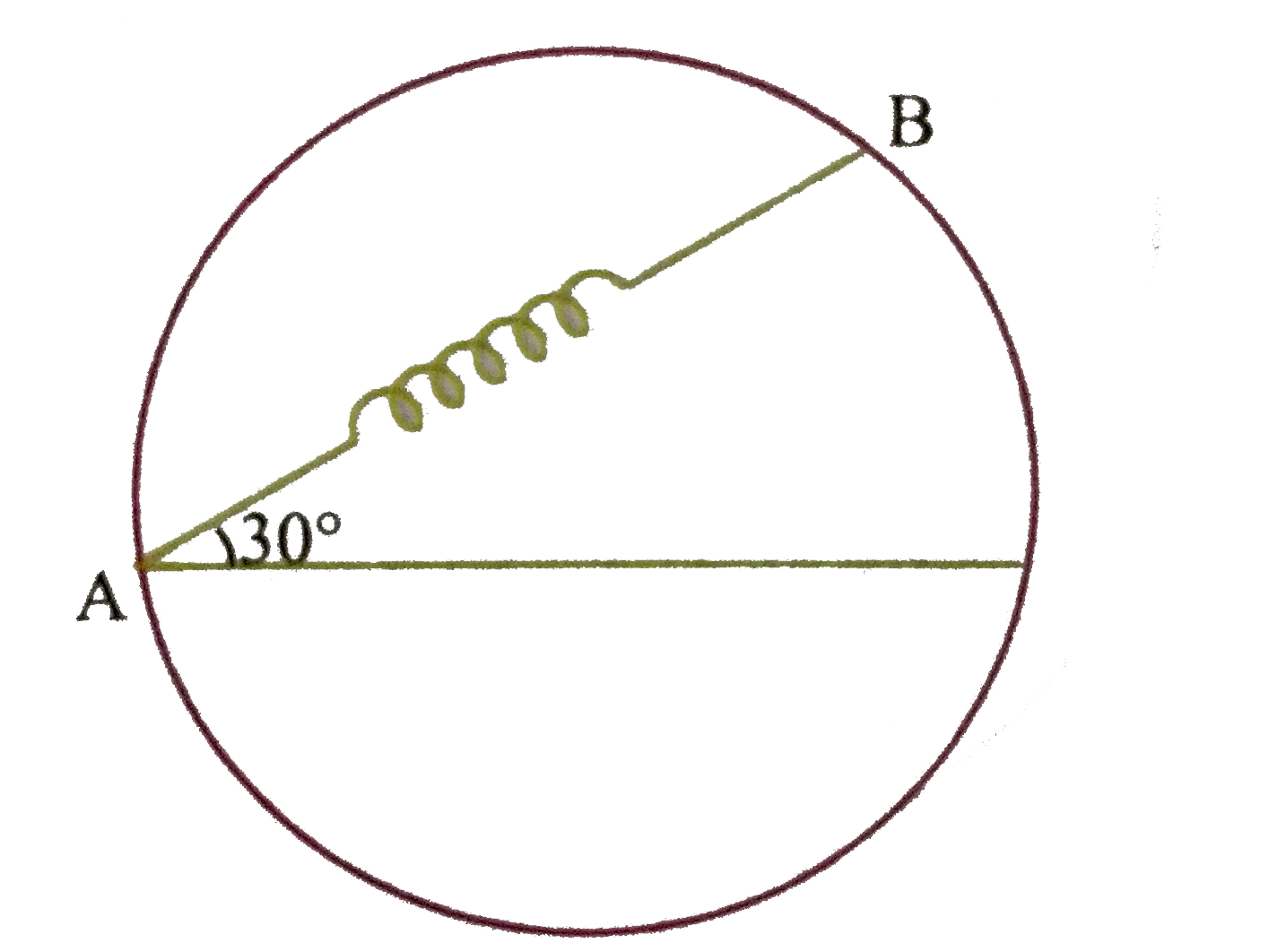
One end of a spring is fixed at point O of a smooth fixed horizontal circular ring of rdius R=2m. A bead having mass 0.3 kg is pivoted on the ring and the other end of spring is connected to it. The natural length of the spring is R and spring constant is k=10N/m.
AB=6R5 and line OB is the diameter of the ring. If the normal reaction on bead due to the ring ag A is 0, what is the speed of the bead at A.
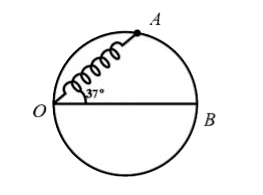
The correct Answer is:08.00
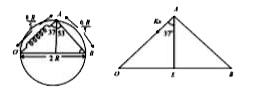
Now for normal force to be zero
Kxcos37=mv2R
x=8R5−R=3R5
Kx3R5×45=0.3×v2R
V=8m/s
Topper's Solved these Questions
Similar Questions
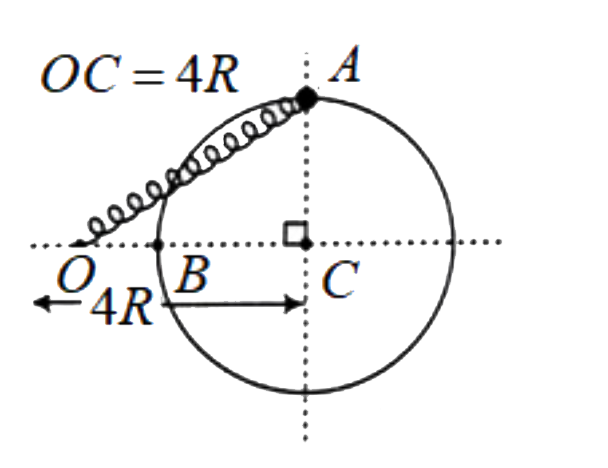
A bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
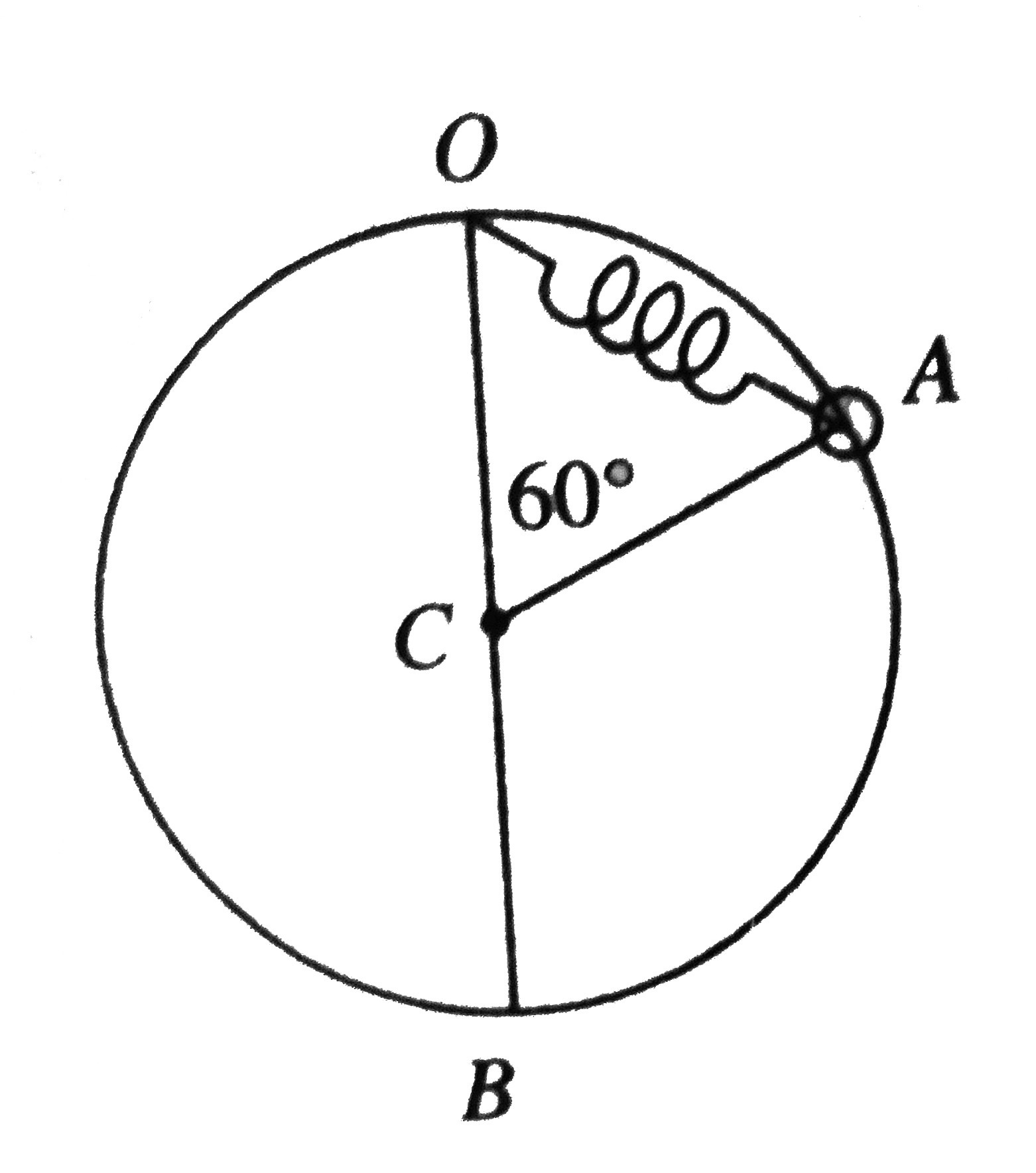
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View Solution
Knowledge Check
A bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
 A252kR2B92kR2C8kR2D12KR2
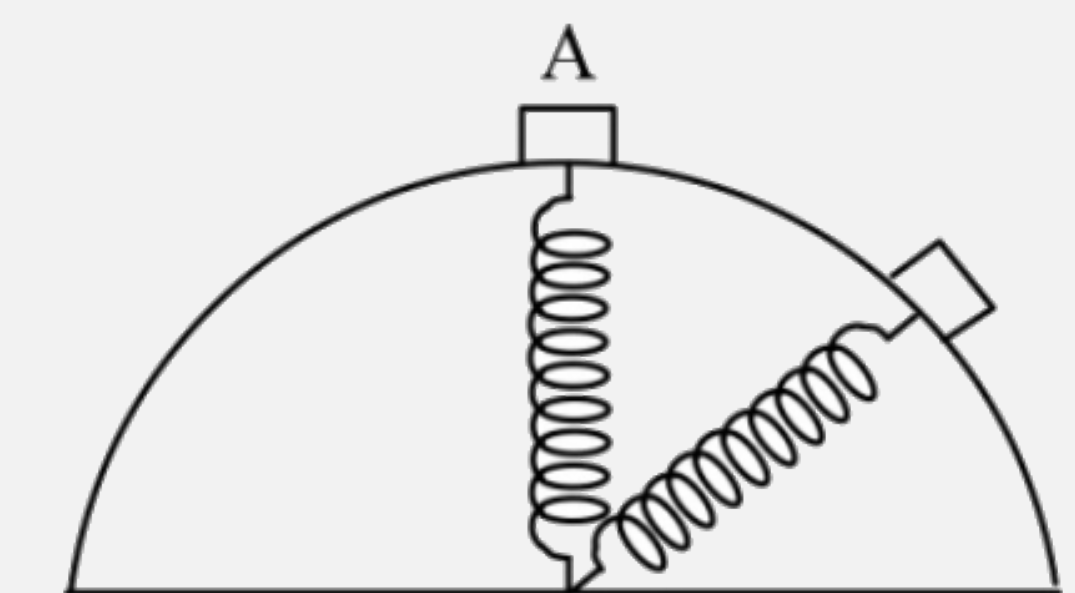
A252kR2B92kR2C8kR2D12KR2A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 Amg/2B√3mgC3√3mgD3√3mg2
Amg/2B√3mgC3√3mgD3√3mg2A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.
AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.
A particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.

View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
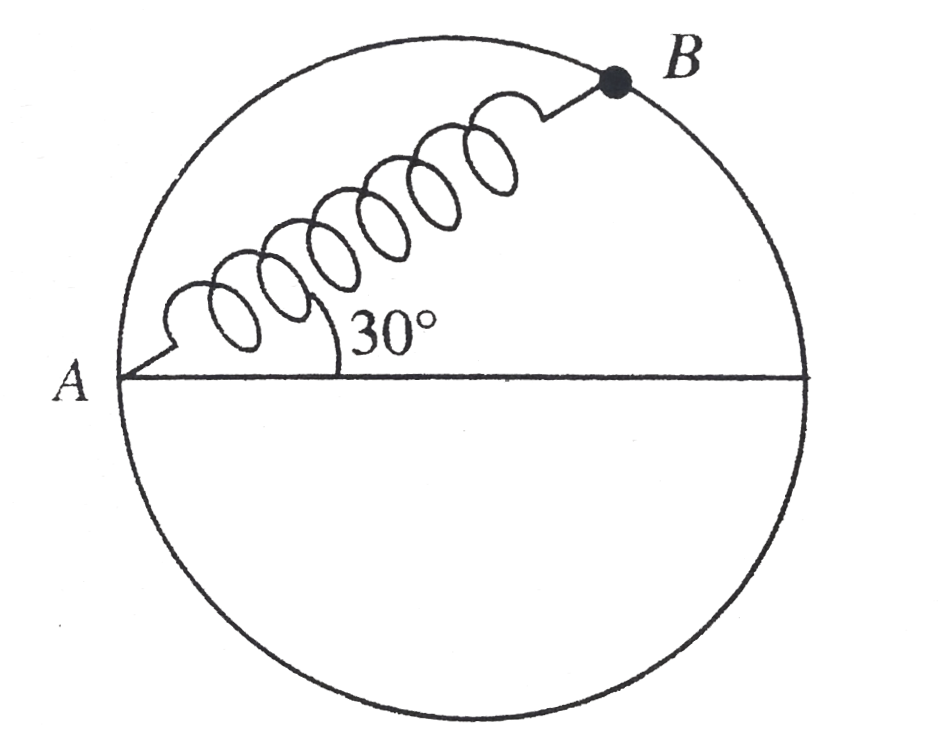
View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is

View Solution
