Three resistors each of resistance 1Ω are connected in parallel. Such connection is again connected with 53Ω resistor in series. The resultant resistant will be ……….Ω
The correct Answer is:2
To find the resultant resistance of the given circuit, we will follow these steps:
Step 1: Calculate the equivalent resistance of the three resistors in parallel.
When resistors are connected in parallel, the formula for the equivalent resistance Rp is given by:
1Rp=1R1+1R2+1R3
In this case, all three resistors have a resistance of 1Ω:
1Rp=11+11+11=3
Thus,
Rp=13Ω
Step 2: Add the equivalent resistance of the parallel combination to the series resistor.
Now, we have the equivalent resistance of the parallel resistors Rp=13Ω and a series resistor of 53Ω. The total resistance Rt in series is given by:
Rt=Rp+Rs
Where Rs=53Ω:
Rt=13+53=1+53=63=2Ω
Final Result
The resultant resistance of the entire circuit is:
2Ω
---
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three resistance of one ohm each are connected in parallel. Such connection is again connected with 2/3Ω resistor in series. The resultant resistance will be
A53ΩB32ΩC1ΩD23ΩIf Four resistors each of 1Ω are connected in parallel the effective resistances will be
A0.5ΩB0.25ΩC4ΩD2ΩA 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.
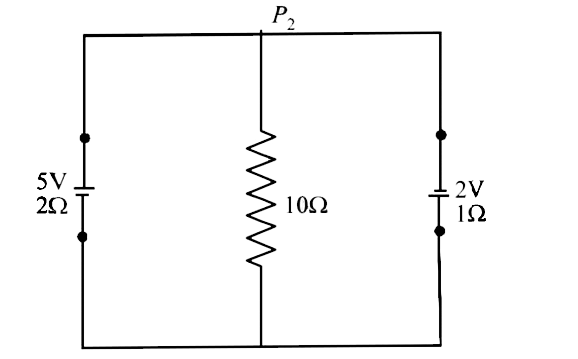
The current in the 10Ω resistor isA0.27 AB0.05 AC0.25 AD0.3 A
These resistors of 10Ω,15Ωand5Ω are connected in parallel. Find their equivalent resistance.
View SolutionThree resistors of 1Ω,2Ωand3Ω are connected in parallel. The combined resistance of 3 resistors should be
View SolutionIf three resistors of resistance 2Ω,4Ω and 5Ω are connected in parallel then the total resistance of the combination will be
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing thrpough the battery ?
View SolutionThree identical resistors, each of 6Ω are connected in parallel. The equivalent resistance of the combination will be ______.
View Solution
