A ball attached to one end of a string is rotated on a horizontal circular path about a vertical axis. Given that the maximum angular velocity of the ball is 42rads−1 a mass (m) of the ball is 0.8 kg, and length (l) of the string is 0.4m. String can bear maximum tension is K×102 then K is
The correct Answer is:5.65
Tcosθ component cancel is mg

Tsinθ component will provide necessqry centripetal force to the ball towards centreO.
∴Tsiθ=mrω2=m(lsinθ)ω2
∴T=m/ω2
∴ω=√Tml
∴ωmax=√Tmaxml
∴Tmax=(ωmax)2×m×l=42×42
×0.8×0.4
∴Tmax=564.48N=5.65×102
Topper's Solved these Questions
Similar Questions
A ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
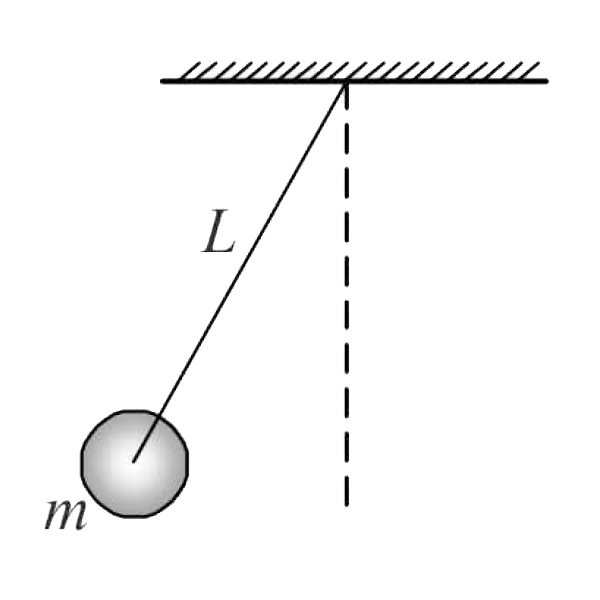
View SolutionA ball of mass (m) 0.5kg is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is

View Solution
Knowledge Check
A ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
 A9B18C27D36
A9B18C27D36A ball of mass 0.25kg attached to the ends of a string of length 1.96m is rotating in a horizonal circle. The string will break, If tension is more than 25N. What is the maximum velocity with which the ball can be rotated ?
A3ms−1B5ms−10C9ms−1D14ms−1A ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (in radian//s) is -
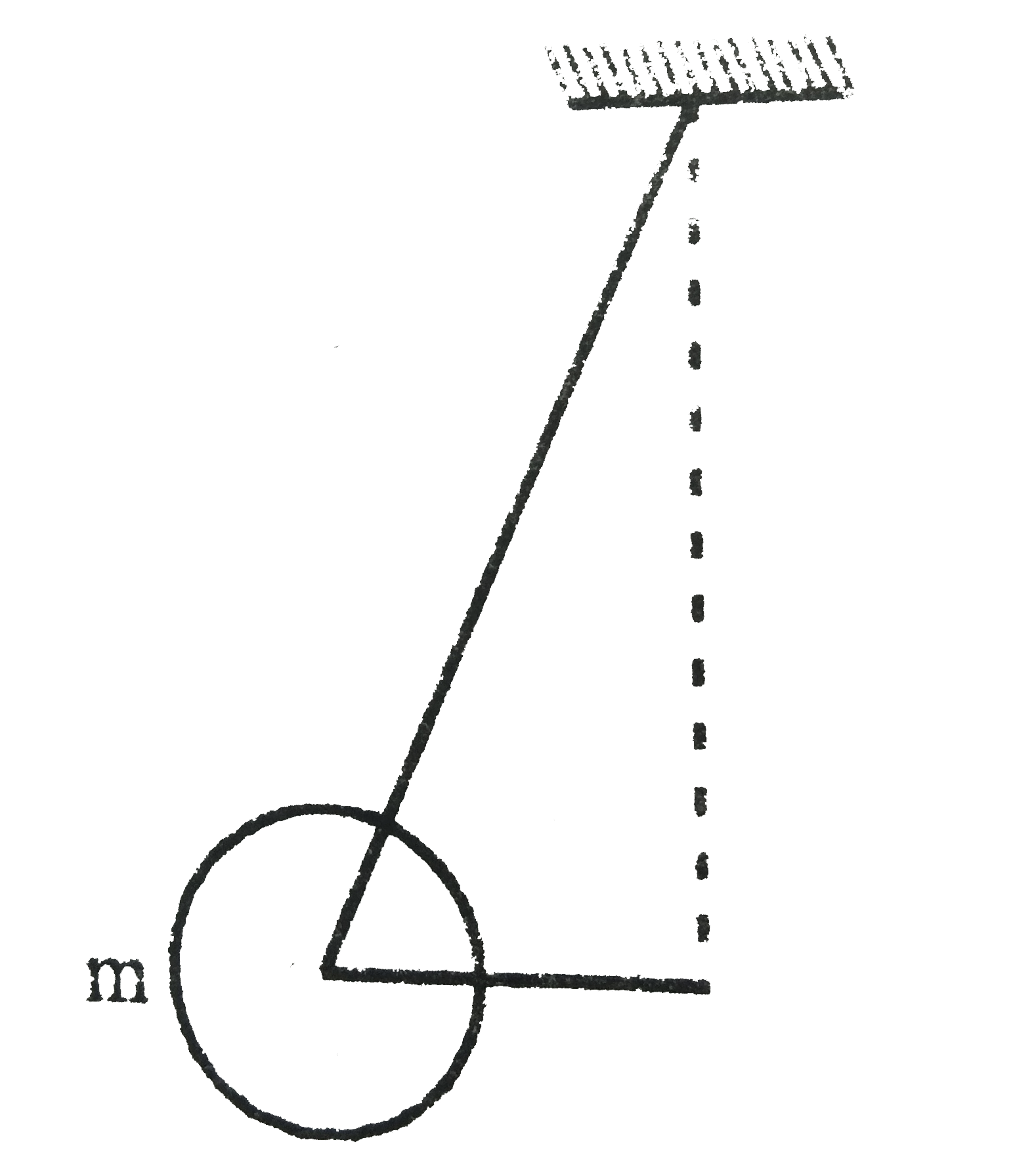 .A9B18C27D36
.A9B18C27D36
A ball of mass m = 0.5 kg is attached to the end of a string having length L = 0.5 is rotated on a horizontal circular path about the vertical axis. The maximum tension that the string can bear is 324N.What is the maximum possible value of angular velocity of ball ( in radian / s ) ?
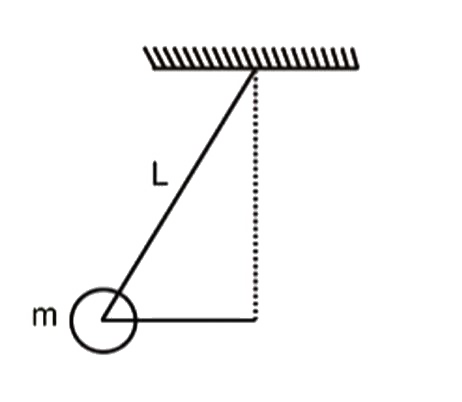
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (in radian//s) is -
 .
.
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (in radian//s) is -
 .
.
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in radian/s) is:
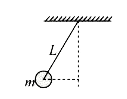
View SolutionStone of mass 1 kg tied to the end of a string of length 1m , is whirled in horizontal circle with a uniform angular velocity 2rads−1. The tension of the string is (in newton)
View Solution
