Consider a wire of radius r and length 2L stretched between two supports A and B without any tension. Now, it is stretched to form AOB as shown in the figure below.The tension is the wire now becomes Cyr2d2L2 where Y is Young's modulus of wire. Now, what is C=? (Take π=3.14)

The correct Answer is:01.57
T=YAlL
Increase in length of one segment of wire
∴T=Yπr2d22L2
⇒C=π2=3.142=1.57
Topper's Solved these Questions
Similar Questions
Two wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a weigth mg, fig. What is the net elonetion in the two wires?
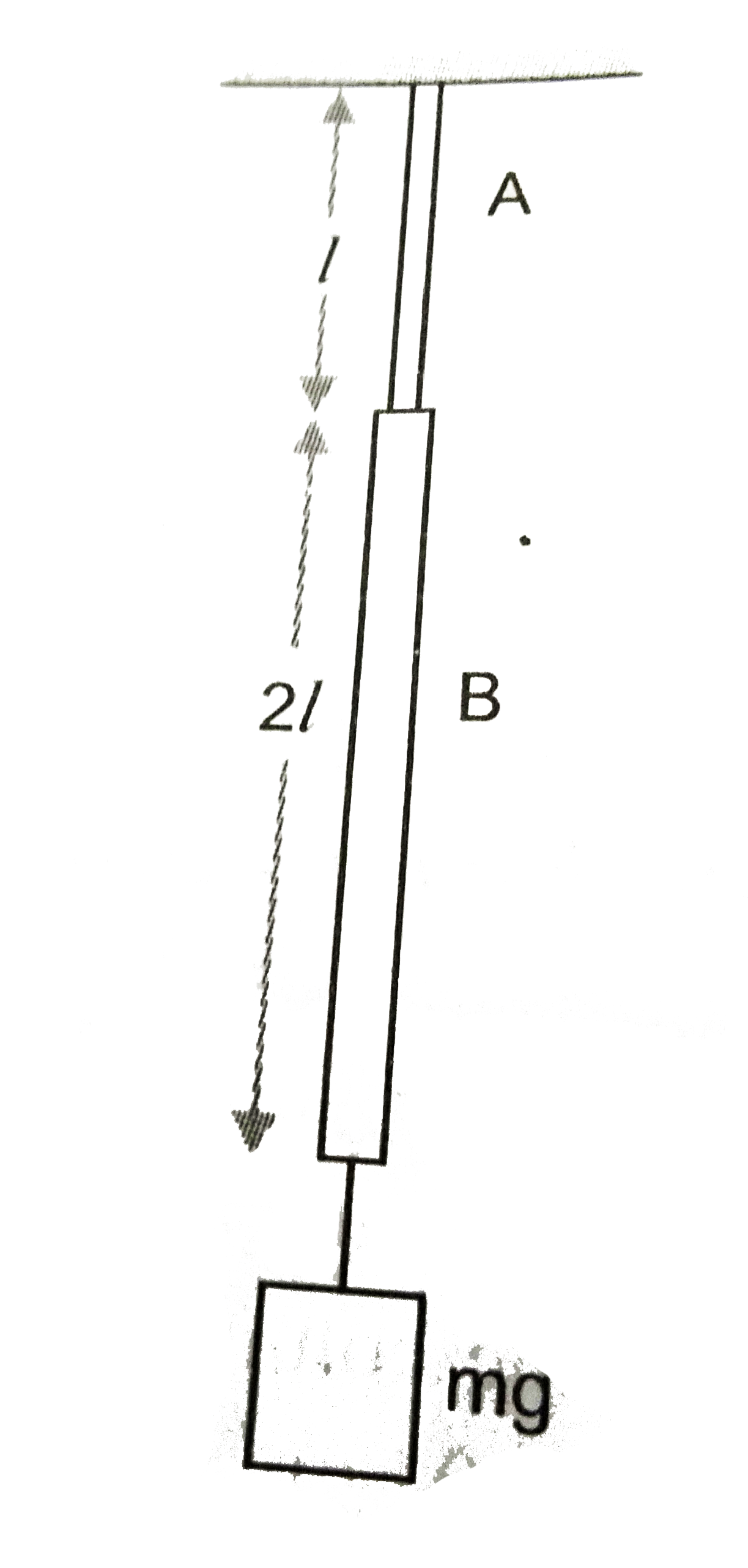
View SolutionTwo wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a width mg, fig. What is the net elongation in the two wires?
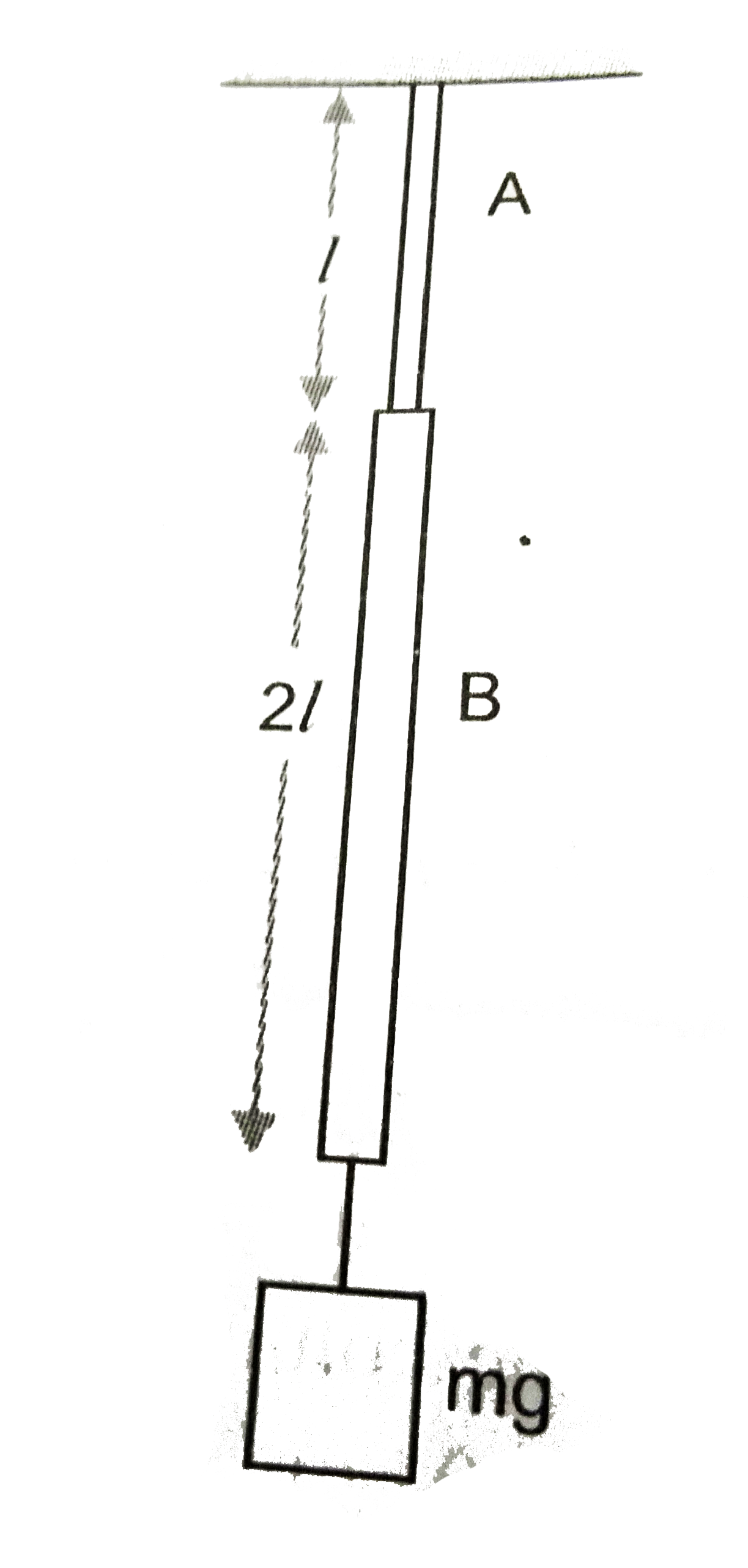
View Solution
Knowledge Check
The resistance of a wire is 2Ω. The wire is stretched to doubel its length. Now the resistance of the wire will become
A0.25RB0.5RC2RD4RLet us consider a copper wire having radius r and length l. Let its resistance be R. If the radius of another copper wire is 2r and the length is l/2 then the resistance of this, wire will be
ARB2RCR/4DR/8The resistance of a wire of length l and diameter d is R. The wire is stretched to double its length. The resistance of the wire will now be
AR2B2RC4RD16R
A wire of radius r stretched without tension along a straight line is tightly fixed at A and B. fig. What is the tension in the wire when it is pulled in the shape ACB? Assume Uoung's modulus of material of the wire to by Y.

View SolutionWhen a wire is stretched and its radius becomes r/2 then its resistance will be
View SolutionA slightly tapring wire of length L and end radii 'a' and 'b' is subjected to stretching forces F, F as shown in

If Y is the Young's Modulus, calculate the extension prouduced in the wire.
View SolutionWhen a wire is stretched and its radius becomes r/2 then its resistance will be
View SolutionA metal wire of circular cross-section has a resistance R. The wire is now stretched without breaking so that its length is doubled and the density is assumed to remain the same. If the resistance of the wire now becomes R2 then R2:R1 is
View Solution
