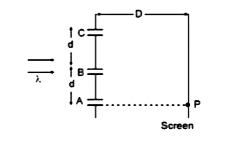
Three equidistant slits are illuminated by a monochromatic parallel beam of light falling normally onto them. The screen is parallel to the plane of the slits and the slit separation d<<D, then slit screen separation. The obsrvation point P is directly opposite A . It is given that BP−AP=λ4,λ being the wavelength of light. Find the ratio of the intensity at P when all slits are open to the intensity at P when only one slit is open.
3
4
5
6
The correct Answer is:C
BP−AP≈d22D=λ4 (given)
CP−AP≈4d22d=λ
Resultant amplitude at P is A. where
A.2=(A+A)2+A2
Topper's Solved these Questions
Similar Questions
figure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.
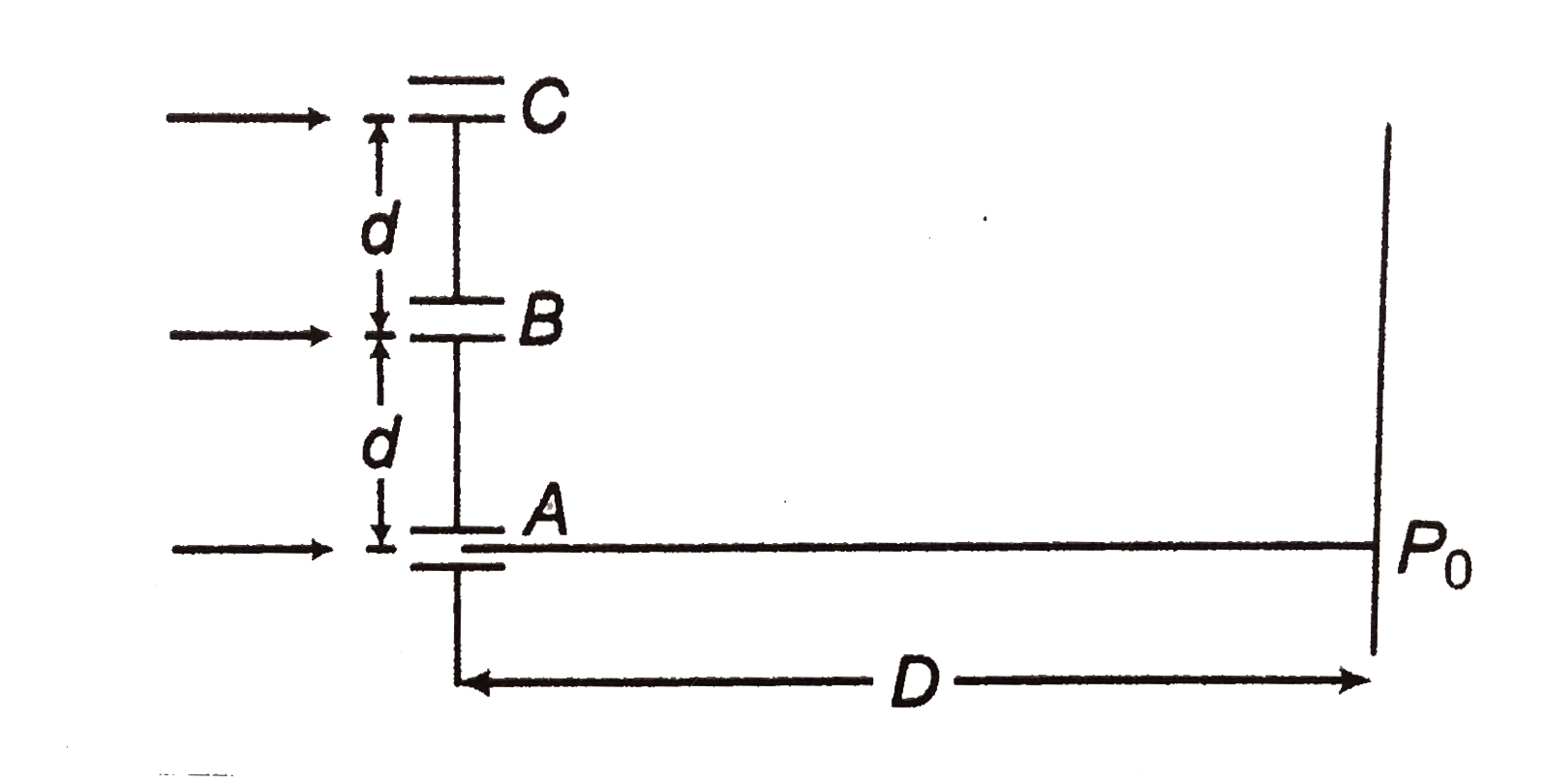
(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.
View Solutionfigure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.

(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.
View Solution
Knowledge Check
S is the size of the slit, d is the separation between the slits and D is the distance of slits from a plane where Young's double slit interference pattern is being observed . If λ be the wavelength of light, then for sharp fringes, the essential conditional is
ASD<λdBSD>λdCSλ<dDDSD>λdA monochromatic light of wavelength λ falls on a single slit. The first secondary maximum occurs at 30∘ if the width of the slit is equal to
Aλ2B3λ2CλD2λ.In a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is λ. The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2. Choose the correct choice (s).
AIf d=λ, The screen will contain only one maximumBIf λ<d<2λ, at least one more maximum (besides the central maximum) will be observed on the screenCIf the intensity of light falling on slit 1 is reduced so that it becomes equal to that of slit 2, the intensities of the observed dark and bright fringes will increaseDIf the intensity of light falling on slit 2 is increased so that it becomes equal to that of slit 1, the intensities of the observed dark and bright fringes will increase
figure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.

(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.
View SolutionIn a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is λ. The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2. Choose the correct choice (s).
View SolutionThree narrow slits A, B and C are illuminated by a parallel beam of light of wavelengthλ , P is a point on the screen exactly in front of point A. Slit plane is at a distance D from the screen(D>>λ). It is know that BP – AP =13
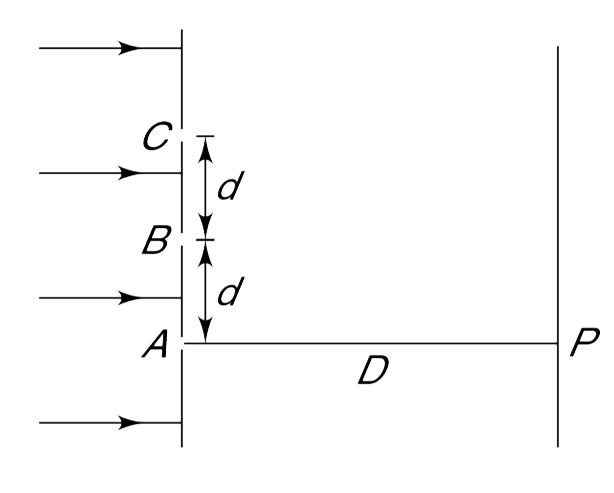
(a) Find d in terms of D andλ
(b) Write the phase difference between waves reaching at P from C and A.
(c) If intensity of P due to any of the three slits individu- ally is I0, find the resultant intensity at P.
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is the intensity of central bright fringe, then intensity at distance from central maximum is
View SolutionIn Young's double slit experiment the two slits are d distance apart. Interference pattern is observed on a screen at a distance D from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is
View Solution
