A train of length l=125 m running on a horizontal surface with its engine switched off starts climbing an inclined track of inclination θ=30∘ as shown in the figure. Total time spent by train or any part of train on inclination is 5πk sec the value of k is (g=10ms−2 assume no loss of energy)
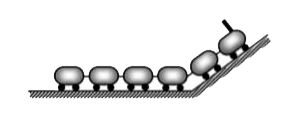
The correct Answer is:1
ma=−(ml.x)gsinθ
a=−(gsinθl)x
⇒d2xdt2=−(gsinθl)x
T=2π√lgsinθ=2π√12510×12⎞⎠=2π
×5=10π sec
Time spent on the inclined track is
t0=T2=10π2=5π sec
Topper's Solved these Questions
Similar Questions
An uniform spherical shell of mass m and radius R starts from rest with pure rolling on long inclined plane as shown in figure. The angular momentum of shell about point of contact after 1 s of its starting is KmR. Determine the value of k(g=10m/s2).
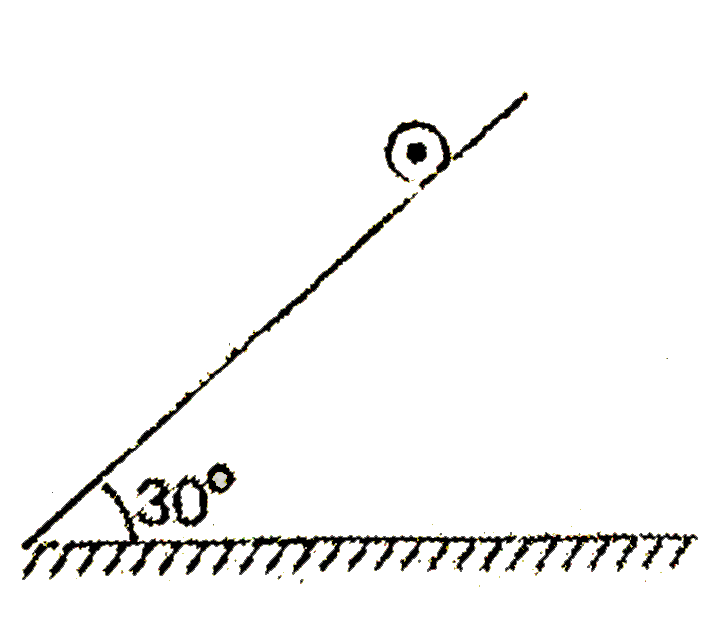
View SolutionAn uniform spherical shell of mass m and radius R starts from rest with pure rolling on long inclined plane as shown in figure. The angular momentum of shell about point of contact after 1 s of its starting is KmR. Determine the value of k(g=10m/s2).

View Solution
Knowledge Check
A block starts going up a rough inclined plane with velocity V0 as shown in figure.After some time reaches to starting point again, with a velocity V02.Find coefficient of friction μ .Given g=10msec2.
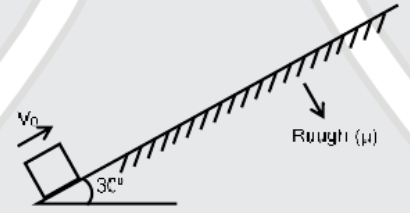 A0.15B0.35C0.75D0.80
A0.15B0.35C0.75D0.80A particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
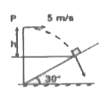 A3.75mB5.0mC4.75mD0.417m
A3.75mB5.0mC4.75mD0.417mA particle is projected up with a velocity of v0=10m/s at an angle of θ0=60∘ with horizontal onto an inclined plane. The angle of inclination of the plane is 30∘. The time of flight of the particle till it strikes the plane is (take g=10ms−2)
A1sB1/2sC2√3sD12√3s
A solid sphere of mass 2 kg and radius R rolls on a smooth horizontal surface at 5ms−1 and then rolls up on a smooth inclined plane of inclination angle 30∘ with horizontal. Calculate the height (in m ) attained by the sphere before it stops.(Take g=10ms−2)
View SolutionA block starts going up a rough inclined plane with velocity V0 as shown in figure.After some time reaches to starting point again, with a velocity V02.Find coefficient of friction μ .Given g=10msec2.

View SolutionA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .

View SolutionRead the given passage and answer the following questions.
A small block of mass M = 1 kg moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point Q. The block is initially at rest at point P. Assume that there is no loss of energy for collisions between the block and the incline. (Take g = 10 m s−2)
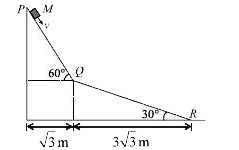
The speed of the block at point Q immediately before it strikes the second incline is
View SolutionA body is allowed to slide from the top along a smooth inclined plane of length 5m at an angle of inclination 30∘.If g=10ms−2, time taken by the body to reach the bottom of the plane is
View Solution
