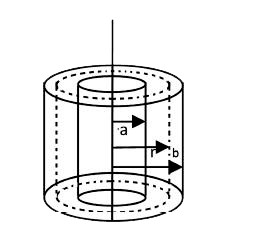
Consider a thick cylinder of inner radius a and b has conductivity sig

Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity $σ$ and a constant potential difference V is maintained between them, by a battery. Then the current, per unit length of the cylinder flowing from one cylinder to the other is
A $\frac{4 π σ}{ln (b / a)} V$
B $\frac{4 π σ}{(b + a)} V$
C $\frac{2 π σ}{ln (b / a)} V$
D $\frac{2 π σ}{(b + a)} V$
Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity $σ$ and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
A $\frac{4 π σ}{ln (b / a)} V$
B $\frac{4 π σ}{b / a} V$
C $\frac{2 π σ}{ln (b / a)} V$
D $\frac{2 π σ}{b + a} V$
Sphere of inner radius a and outer radius b is made of $p$ uniform resistivity find resistance between inner and outer surface
A $\frac{p}{4 π} (\frac{1}{a} - \frac{1}{b})$
B $\frac{p}{2 π} (\frac{1}{a} - \frac{1}{b})$
C $\frac{p}{3 π} (\frac{2}{a} - \frac{1}{b})$
D $\frac{p}{2 π} (\frac{2}{2 a} - \frac{1}{b})$

Consider a thick cylinder of inner radius a and b has conductivity $σ .$ A battery of emf V is connected between the inner and outer surface of the cyllinder. Find the current flowing, per unit length of the cylinder