A source that is 0.10 m away from a fresnel biprism of angle 2∘ which illuminated by the light of wavelength 6280Å. What will be the width of the fringes(inmm) formed on a screen kept 0.9 m away from the biprism? (Take Refracive index of glass =1.5π=3.14)
The correct Answer is:0.18
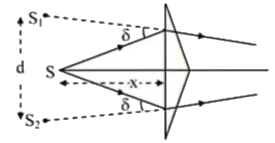
The deviation δ produced by each half of biprims =(μ−1)A
where A is in radian.
Here
d=2(μ−1)Ax
=2(1.5−1)(π180×2∘)×0.1
d=π900m
D=0.9+0.1=1m
Now β=λDd
β=(6280×10−10)×1π900=1.8×10−4m=0
.18mm
Topper's Solved these Questions
Similar Questions
Two slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
View SolutionThe distance between a slit and a biprism of acute angle 2∘ is 10 cm. Find (a) the fringe width and (b) the width of the entire fringe pattern when observation is made on screen at a distance of 90 cm from the biprism. The refractive index of the biprism is 1.5 and l = 5890 Å.
View Solution
Knowledge Check
Two slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
A0.12mmB0.3mmC3.0mmD4.0mmTwo parallel slits 0.6mm apart are illuminated by light source of wavelength 6000Å. The distance between two consecutive dark fringe on a screen 1m away from the slits is
A(a) 1mmB(b) 0.01mmC(c) 0.1mD(d) 10mThe obtuse angle of Fresnel's biprism is 178∘. A slit is illuminated by light to wavelenght 6000Å is at distance of 10 cm from the biprism. Find the fringe widht on a screen at a distance of 90 cm from the biprism . The refractive index of the material of the birism is 1.5
A0.000344mmB0.0034mmC0.034mmD0.34mm
Light of wavelength 5500 Å falls on a slit on a slit of width 0.13 cm at normal incidence. Calculate the width of the central maximum on a screen kept 2.5 m away from slit.
View SolutionThe distance between a slit and a biprism of acute angle 2∘ is 10cm. Find the fringe width and the width of the entire band when observation is made on a screen at a distance of 90 cm from the biprism. The refractive index of the material of the biprism is 1.5 and λ=5890Å.
View SolutionIn a biprism experiement, by using light of wavelength 5000Å, 5mm wide fringes are obtained on a screen 1.0m away from the coherent sources. The separation between the two coherent sources is
View SolutionIn Young's experiment, interference bands are produced on the screen placed at 1.5 m from the two slits 0.15 mm apart and illuminated by light of wavelength 6599Å. Find (a) the fringe width and (b) the change in the fringe width if the screen is taken away from the slit by 50 cm.
View SolutionIn a biprism experiement, by using light of wavelength 5000Å, 5mm wide fringes are obtained on a screen 1.0m away from the coherent sources. The separation between the two coherent sources is
View Solution
