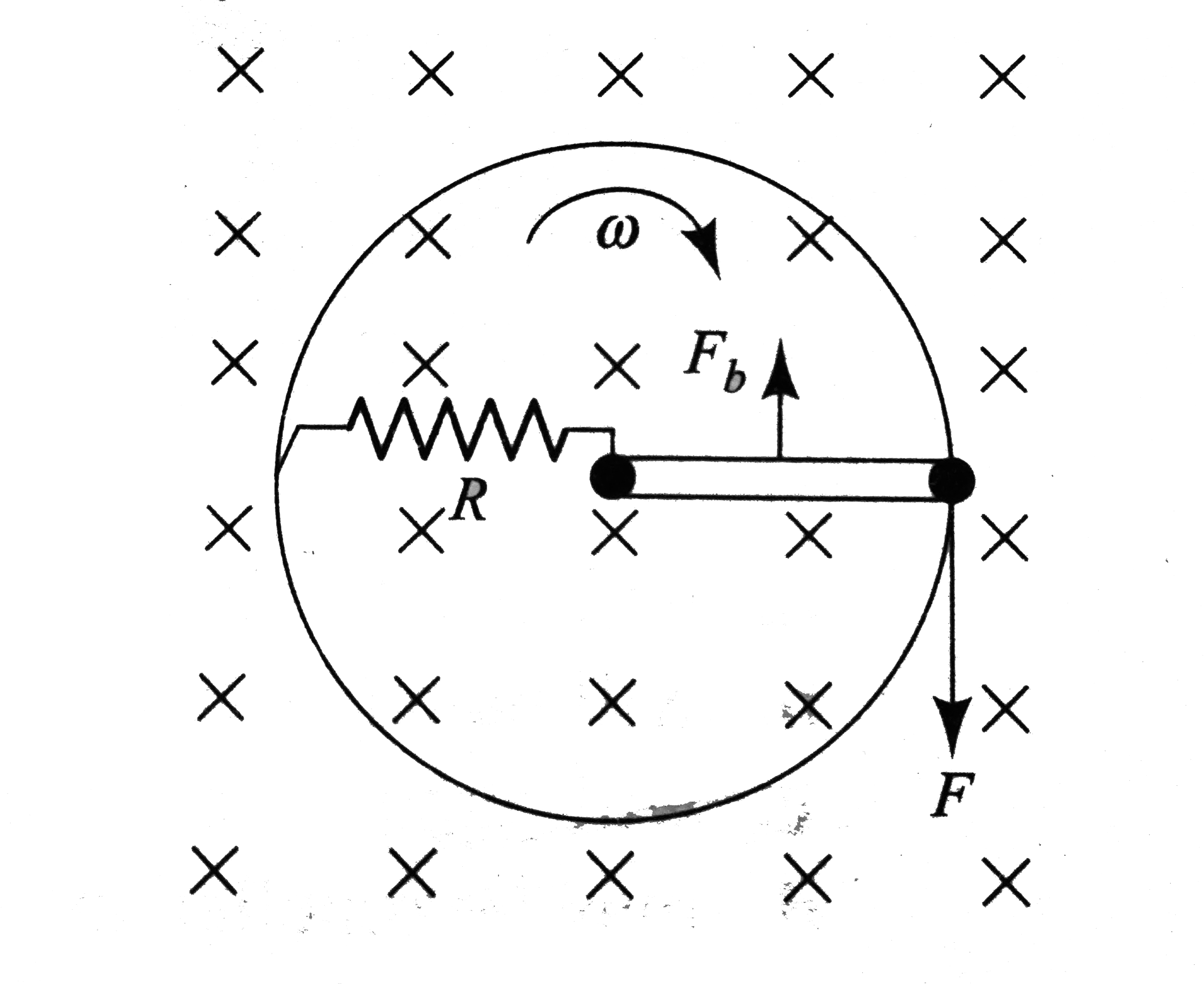
A metallic ring of radius $r$ with a uniform metallic spoke of negligible mass and length $r$ is rotated about its axis with angular velocity $ω$ in a perpendicular uniform magnetic field $B$ as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor $R$ as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. $F$ is equal to (the ring and the spoke has zero resistance)

A

$\frac{B^{2} ω r^{2}}{8 R}$

B

$\frac{B^{2} ω r^{2}}{2 R}$

C

$\frac{B^{2} ω r^{3}}{2 R}$

D

$\frac{B^{2} ω r^{3}}{4 R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$F_{b} = B I L$
Induced current
$I = \frac{B ω r^{2} / 2}{R}$

$∴ F_{b} = B \frac{B ω r^{2}}{2 R} r = \frac{B^{2} ω r^{3}}{2 R}$
To maintain constant angular velocity:
$F (r) = F_{B} (\frac{r}{2}) \Rightarrow F = \frac{F_{B}}{2} = \frac{B^{2} ω r^{3}}{4 R}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A non-conducting disk of radius $R$ is rotating about its own axis with constant angular velocity $ω$ in a perpendicular uniform magnetic field $B$ as shown in figure. The emf induced between centre and rim of disk is

A $\frac{B ω R^{2}}{2}$
B $B ω R^{2}$
CZero
D $\frac{B ω R^{2}}{3}$
Question 2 - Select One
A metallic ring of radius $r$ with a uniform metallic spoke of negligible mass and length $r$ is rotated about its axis with angular velocity $ω$ in a perpendicular uniform magnetic field $B$ as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor $R$ as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. $F$ is equal to (the ring and the spoke has zero resistance)

A $\frac{B^{2} ω r^{2}}{8 R}$
B $\frac{B^{2} ω r^{2}}{2 R}$
C $\frac{B^{2} ω r^{3}}{2 R}$
D $\frac{B^{2} ω r^{3}}{4 R}$
Question 3 - Select One
A horizontal ring of radius $r$ spins about its axis with an angular velocity $ω$ in a uniform vertical magnetic field of magnitude $B$ . The emf induced in the ring is
Azero
B $π r^{2} ω B$
C $\frac{1}{2} B r^{2} ω$
D $B r^{2} ω$

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 57-PHYSICS

Home
Ask Doubt
Profile