A metal bar AB can slide without friction on two parallel thick metallic rails separated by a distance I. A resistance R and an inductance L are connected to the rails as shown in the figure. An infinite long straight wire carrying a constant current I0 is placed on the plane of the rails as shown. The bar AB is held at rest at a distance x0 from the long wire. At t = 0, it is made to slide on the rails away from the wire.
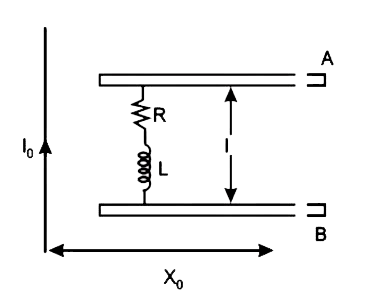
It is observed that at time t = T, the metal bar AB is at a distance of 2x0 from the long wire and the resistance R carries a current ix. Obtain an expression for the net charge that has flown through resistance R from t = 0 to t = T.
1R[μ0I2πln(2)−Li1]
1R[l2πI0ln(2)−Li1]
1R[μ0I0l2πln(2)−Li1]
1R[μ0I02πln(2)−Li1]
The correct Answer is:C
Let V be velocity of AB when AB is at a distance x. from the wire,
eAB=B.l.v=μ0I02πxI.V=dϕdt
For circuit loop,
dϕdt−iR−Ldidt=0
⇒dq=dϕ−LdiR
Δq=Δϕ−LΔlR = change flown
=1R[(ϕ1−ϕ2)−L(I1)]
If ϕ1= Final flux through circuit when x=2x0.
ϕ2 = Final flux through circuit when x=x0
Δq=1R[μ0lI1ln(2)2π−Ll1]
Topper's Solved these Questions
Similar Questions
A metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
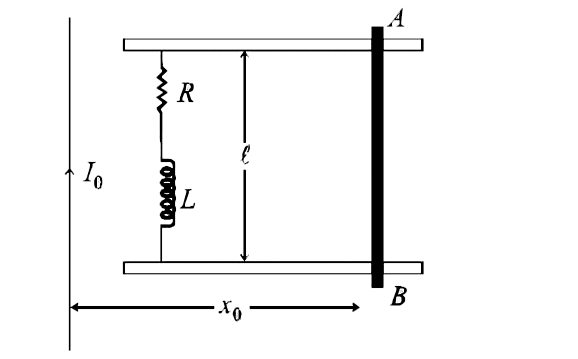
View SolutionA metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.

View Solution
Knowledge Check
The magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2iMagnetic field at a distance r from an infinitely long straight conductor carrying steady varies as
Aμ04π2IrBμ04πIrCμ0IπrD2μ0IπrA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
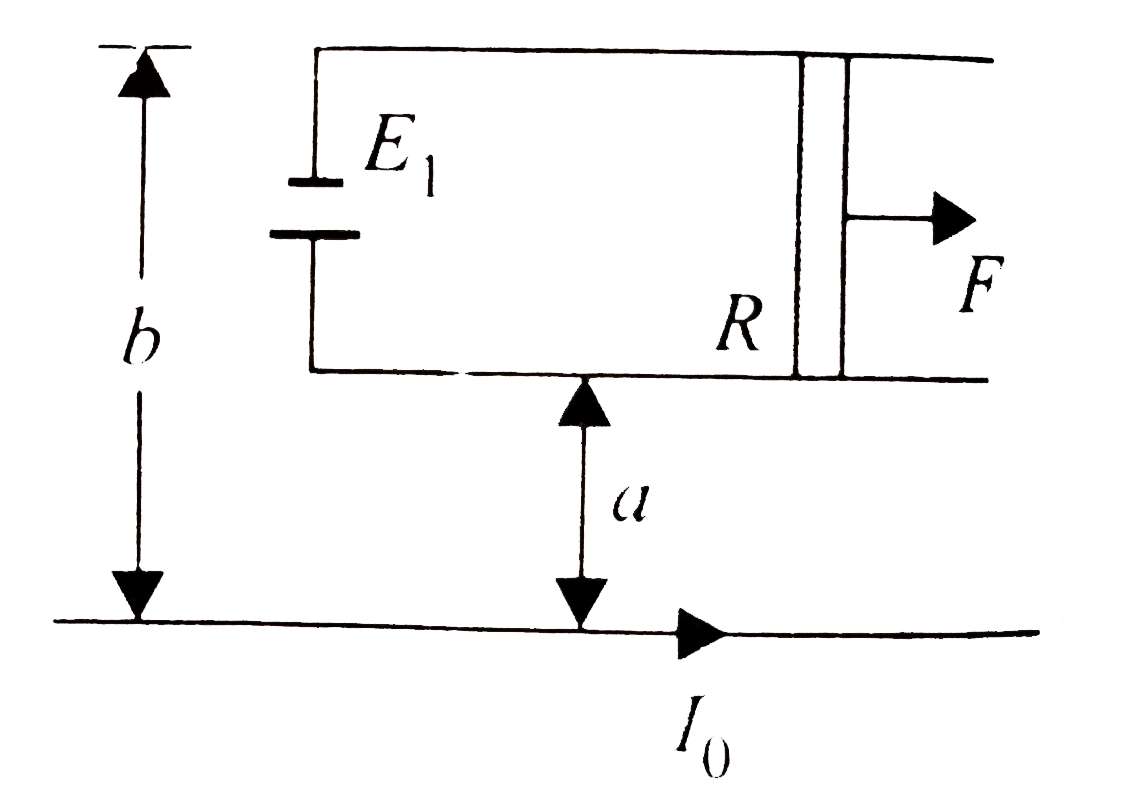
Find the value of current in the circuit if the rod slides with constant velocity v0A1R{E−μ0I0v02π1n∣∣∣ba∣∣∣}B1R{E+μ0I0v02π1n∣∣∣ba∣∣∣}C1R{E−μ0I0v0π1n∣∣∣ba∣∣∣}DNone of these
A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.

Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
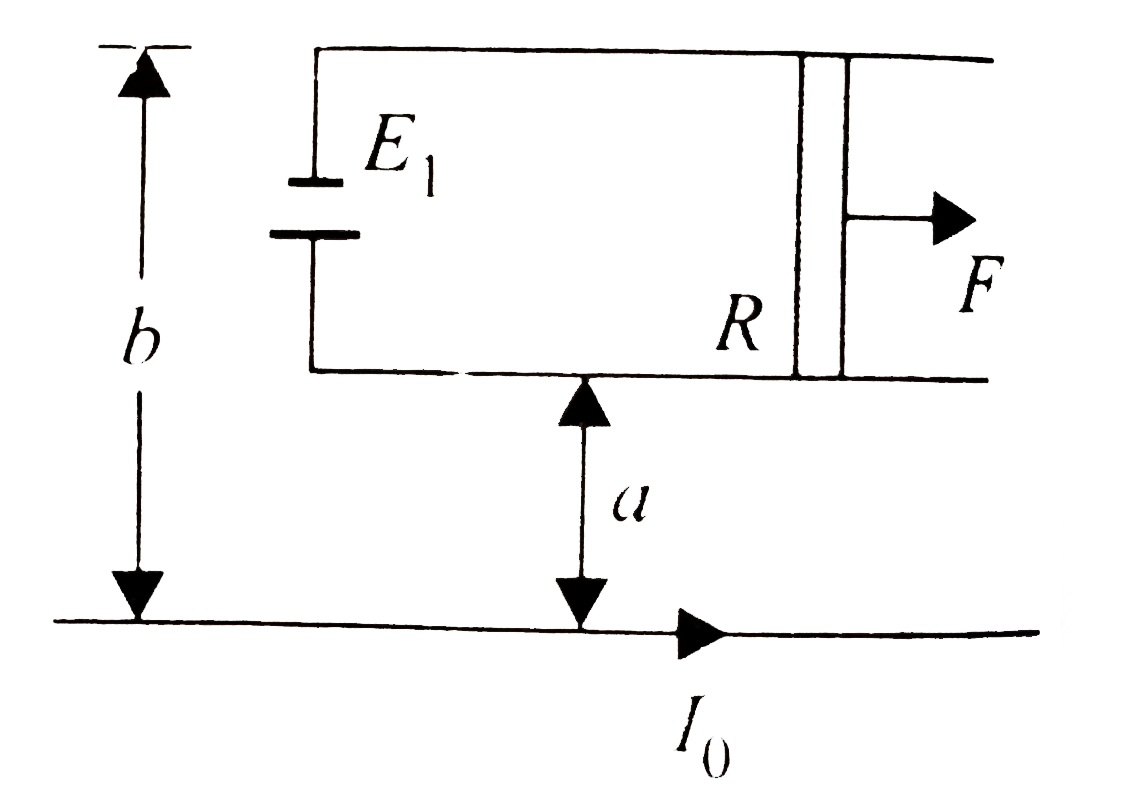
Find the value of F if the rod slides with constant velocity
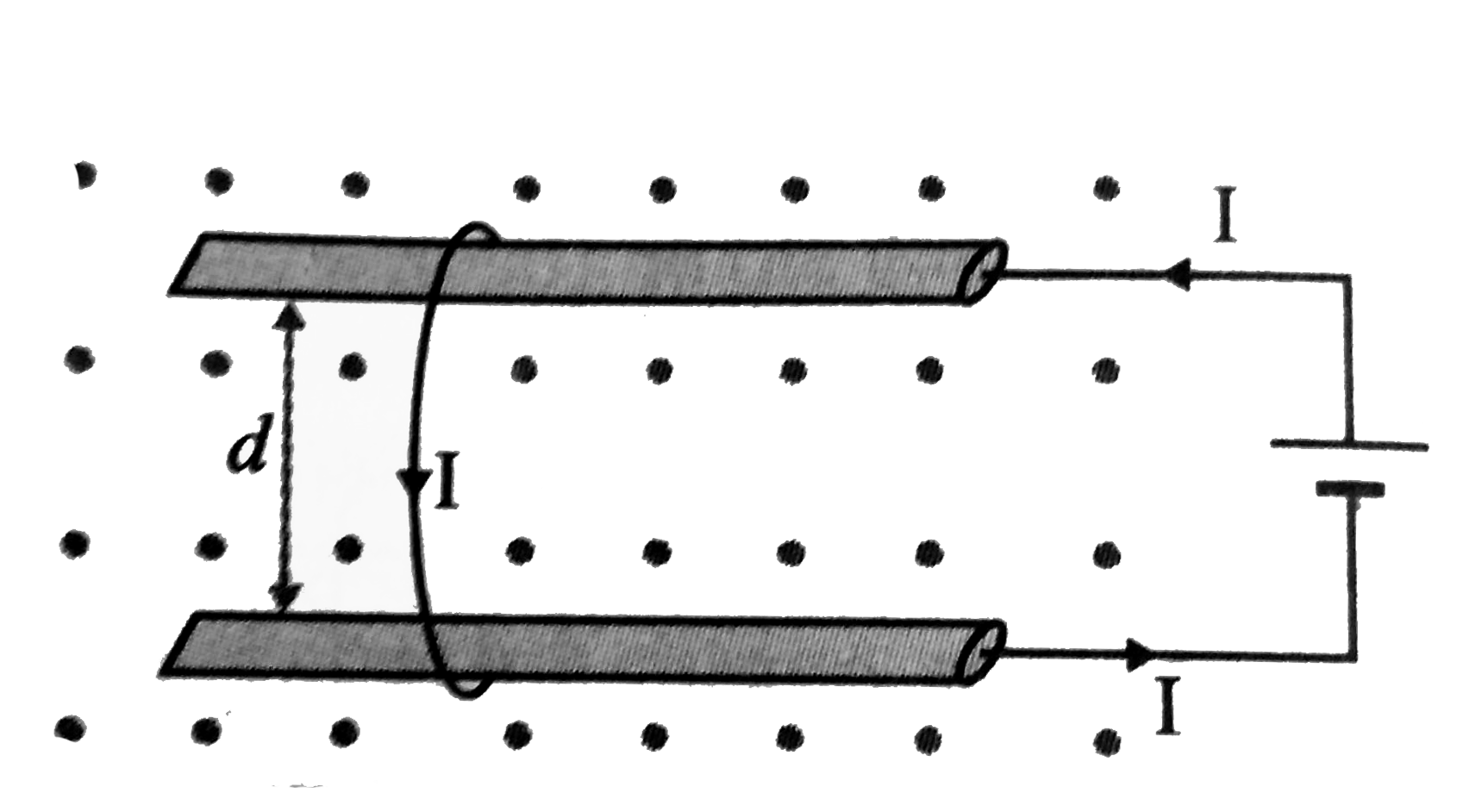
View SolutionA metal wire of mass m slides without friction on two horizontal rails spaced distance d-apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upwards, and a battery is sending a current I through them. Find the velocity of the wire as a function of time, assuming it to be at rest initially.
View SolutionA bar of mass m slides on a smooth horizontal conducting rail. A constant current I is maintained in the rod using a constant current generator as shown. There is a long straight conductor carrying current I0 parallel to the rod. Find the speed of the bar after it has travelled a distance D

View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.

Find the value of F if the rod slides with constant velocity
View Solution
