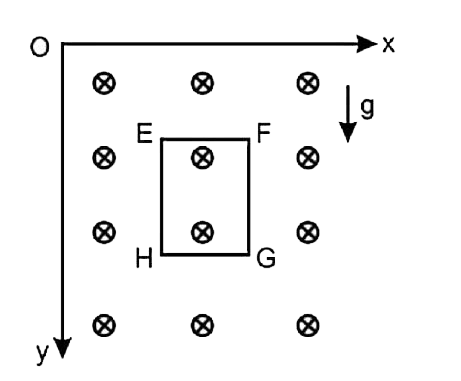
A magnetic field B=(B0y/a)ˆk is acting into the paper in the + z direction. Bo and a are positive constants. A square loop EFGH of side a, mass m and resistance R kept in x-y plane starts falling under the influence of gravity. Note the directions of x and y in the figure.
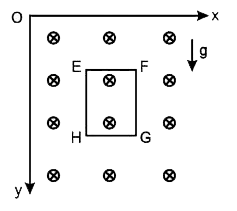
Find the total Lorentz force acting on the loop and indicate its direction.
→F=B20a2vRˆj upwards
→F=B20a2vRˆj downwards
→F=B20a2vRˆj upwards
→F=B20a2vRˆj downwards
The correct Answer is:C
When the side EF is at a distance y from the x-axis, magnetic flux that is passing through the loop is

ϕ=∫dϕ=∫Y=y+aY=ya0Ya(adY)
ϕ=B02[(y+a)2−y2]
Induced emf is
e=∣∣∣−dϕdt∣∣∣=∣∣∣−Bα2[2(y+a)−2y]dydt∣∣∣
e=B0adydt
e=B0va where v=dydt = speed of loop
∴ Induced current I=eR=B0avR
Direction: ∣∣→B∣∣∝y i.e., as the loop comes down ⊗ magnetic field passing through the loop increases, therefore the induced current will produce ⊙ magnetic field or the induced current in the loop will be counter-clockwise. Alternate solution
Motional emf in EH and FG = 0 as
→V∣∣→0
Motional emf in EF is e1 =
(B0ya)(a)v=B0yv
(e=Blv)
Similarly motional emf in GH will be
e2={B0(y+a)a}(a)(v)=B0(ay)v
Polarities of e1 and e2 are shown in adjoining figures.
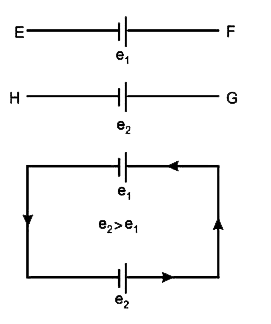
Net emf,
e=e2−e1
e=B0av
i=eR=B0avR
and direction of current will be counter clockwise.
Total Lorentz force on the loop:
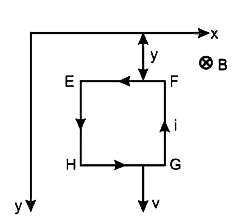
We have seen in part (a) that induced current passing through the loop (when its speed is v) is
I=B0avR
Now magnetic force on EH and FG are equal in magnitude and in opposite directions, hence they cancel each other and produce no force on the loop.
FEF=(B0avR)(a)(B0ya)(downwards)
(f=ilB)=B20avyR
and
FGH=(B0avR)(a)(B0(y+a)a)(upwards)
=(B20avR)(y+a)
FGH>FEF
∴ Net lorentz force on the loop
=FGH−FEF=(B20a2vR)ˆj
→F=−a20a2vRˆj
Topper's Solved these Questions
Similar Questions
A magnetic field B=B0(y/a)(^)k is into the paper in the +z direction, B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x-y plane, starts falling under the influence of gravity see figure. Note the direction of x and y axis in figure.
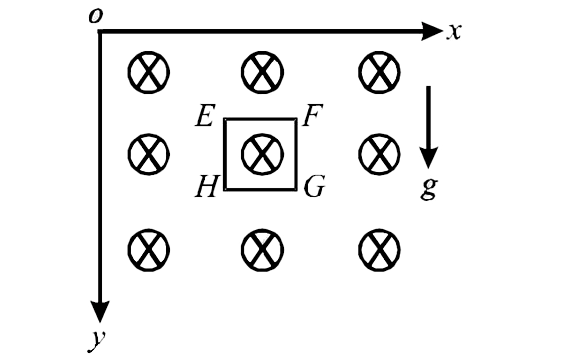
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
(c) an expression for the speed of the loop, v(t) and its terminal value.View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View Solution
Knowledge Check
- Question 1 - Select One
A magnetic field B=(B0y/a)ˆk is acting into the paper in the +z direction. B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R kept in x-y plane starts faling under the influcence of gravity.Note the directions of x and y in the figure.
Find the induced current in the loop and indicate its direction.Ai=B0avR and direction of current will be counter clockwiseBi=RB0av and direction is counter clockwiseCi=B0avR and direction is clockwiseDi=RB0av and direction is clockwise - Question 2 - Select One
A circular loop with N turns has radius r . It lies in the x-y plane carrying current I in the anti-clockwise direction . If the magnetic field in the region is →B=B0ˆi , then find the torque (→r) acting on the loop .
AB0NIπr2ˆjBB0Iπr2ˆjCB0NIπr2ˆkDB0πr2atk - Question 3 - Select One
In x-y plane, a force 10N acts at an angle 30∘ to the positive direction of x-axis. The force can be written as
A5ˆi+5ˆjB5√3ˆi+5ˆjNC5ˆi+5√3ˆjNDNone of these
A current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA circular loop with N turns has radius r . It lies in the x-y plane carrying current I in the anti-clockwise direction . If the magnetic field in the region is →B=B0ˆi , then find the torque (→r) acting on the loop .
View SolutionIn x-y plane, a force 10N acts at an angle 30∘ to the positive direction of x-axis. The force can be written as
View SolutionA square shaped current loop of side length L and carrying current I lies in a uniform magnetic field B acting perpendicular to the plane of squre loop and directed inward. The net magnetic force acting on current loop is
View SolutionA square shaped current loop of side length L and carrying current I lies in a uniform magnetic field B acting perpendicular to the plane of squre loop and directed inward. The net magnetic force acting on current loop is
View Solution

