सभी खण्ड कीजिए-
एक ΔABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि ∠ADC=∠BAC है तो सिद्ध करो CA2=CB×CD
Step by step video & image solution for सभी खण्ड कीजिए- एक DeltaABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि angleADC=angleBAC है तो सिद्ध करो CA^2=CB×CD by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
3x4+6x3−2x2−10x−5 के सभी अन्य शून्यक ज्ञात कीजिए, यदि इसको दो शून्यक −√53 और √53 हैं।
View Solutionr त्रिज्या वाले वृत के एक त्रिज्यखण्ड का केंद्रीय कोण θ है। इस त्रिज्यखण्ड का क्षेत्रफल है--
View Solutionएक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC=∠BAC है । दर्शाइए कि CA2=CB⋅CD है ।
View Solutionचित्र 1 में त्रिभुज ABC की भुजा BC पर बिन्दु D इस प्रकार है कि ∠ADC=∠BAC, तो सिद्ध कीजिए CACD=CBCA
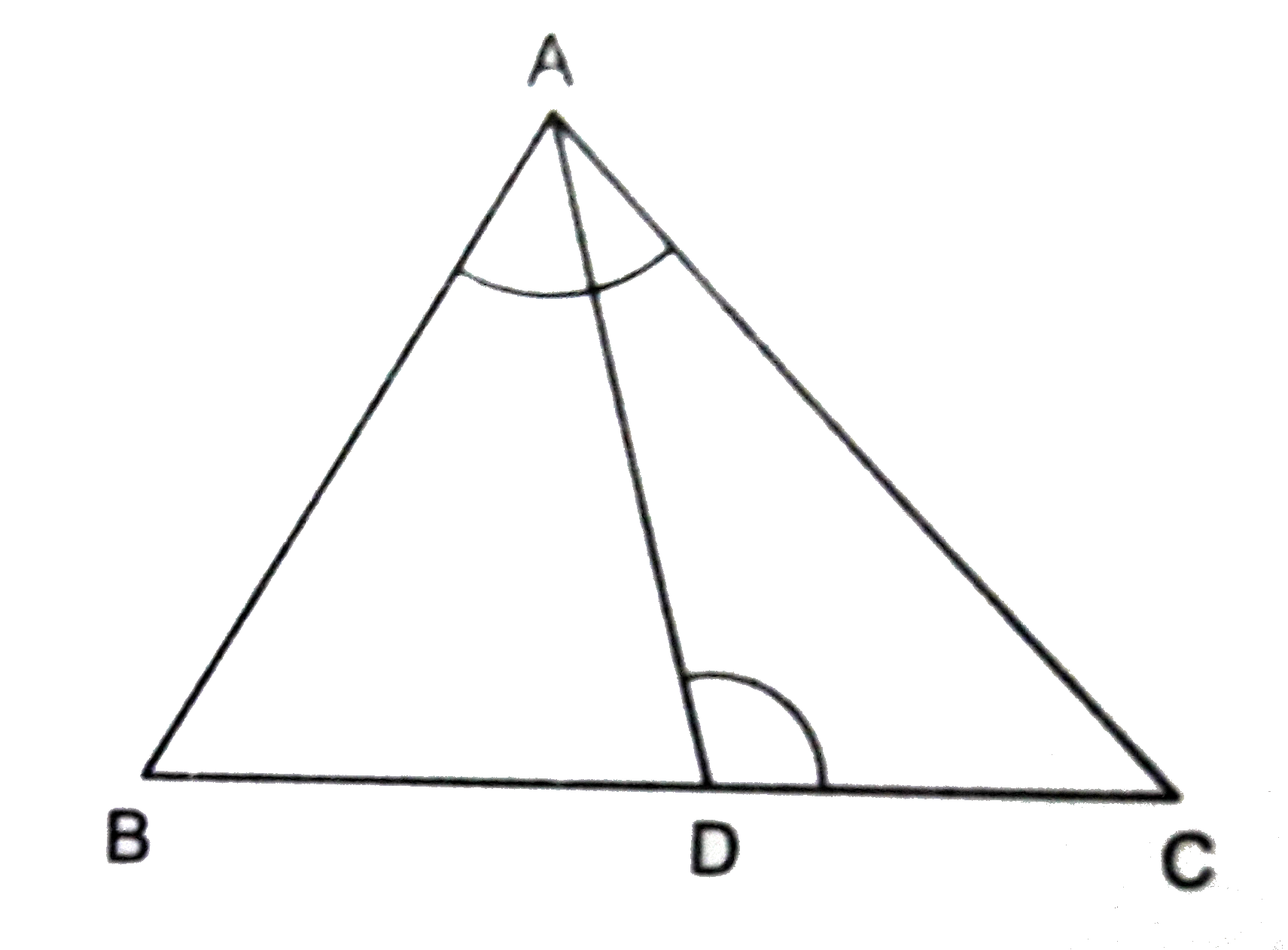
View SolutionIn the adjoining figure, in ΔABC, point D is on side BC such that, ∠BAC=∠ADC. Prove that, CA2=CB×CD.
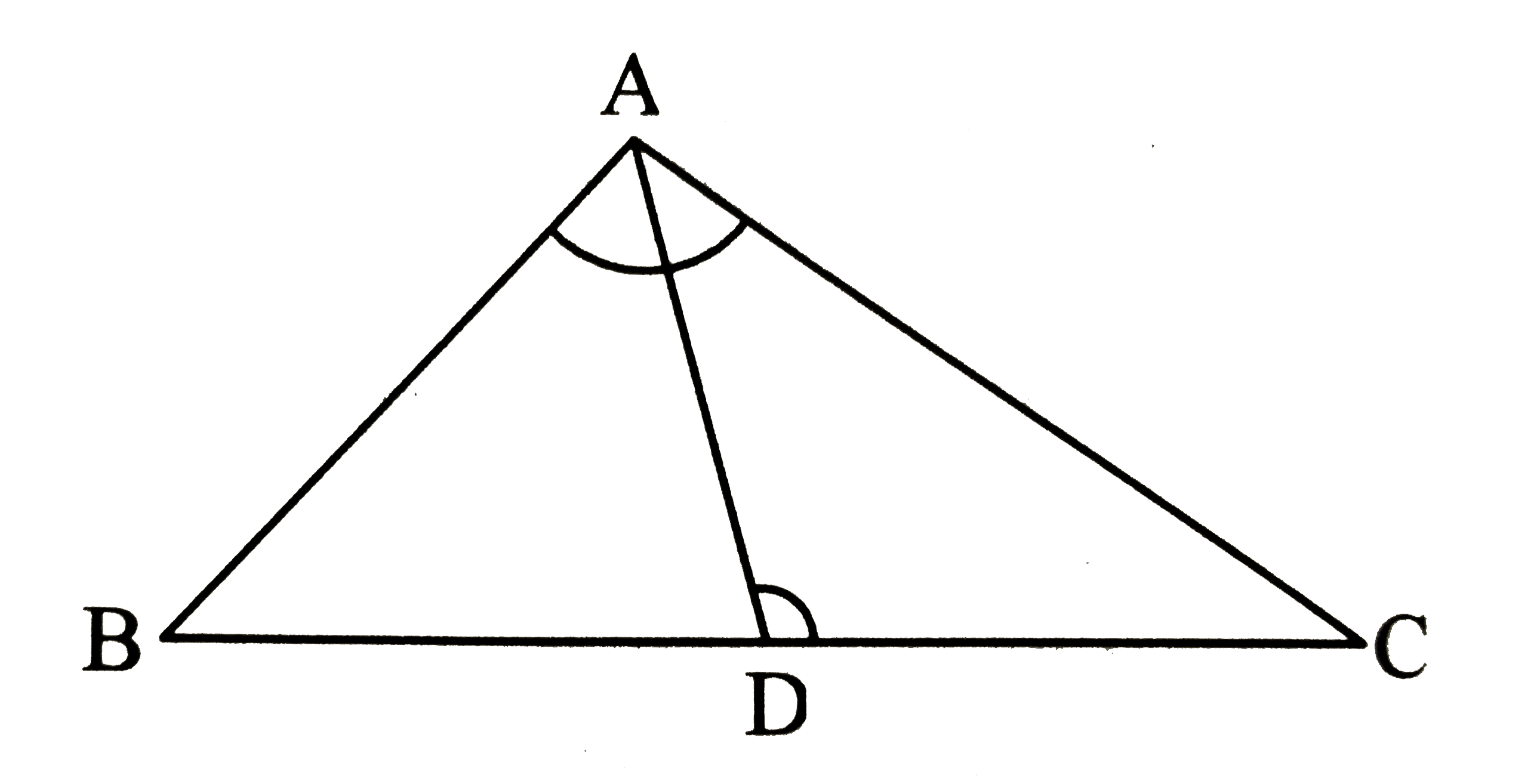
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC . Show that CA2 = CB. CD.
View Solution
