What is inflection point ?
Inflection point is the point on the total cost curve where marginal cost is minimum.
Inflection point is the point on the total cost curve where marginal cost is greater than zero.
Inflection point is the point on the total cost curve where marginal cost is zero.
Inflection point is the point on the total cost curve where marginal cost is maximum.
The correct Answer is:A
Topper's Solved these Questions
- APPLICATION OF CALCULUSBOOK - ICSECHAPTER - APPLICATION OF CALCULUSEXERCISE - Assertion and Reason based questions
5 Videos
- APPLICATION OF CALCULUSBOOK - ICSECHAPTER - APPLICATION OF CALCULUSEXERCISE - Competency based questions
10 Videos
- APPLICATION OF CALCULUS IN COMMERCE AND ECONOMICSBOOK - ICSECHAPTER - APPLICATION OF CALCULUS IN COMMERCE AND ECONOMICSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
14 Videos
Similar Questions
Knowledge Check
An equation of tangent line at an inflection point of f(x)=x4−6x3+12x2−8x+3 is
Ay=3x+4By=4Cy=3x+2Dnone of theseThe number of inflection points of a function given by a third degree polynomial is exactly
A2B1C3D0Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
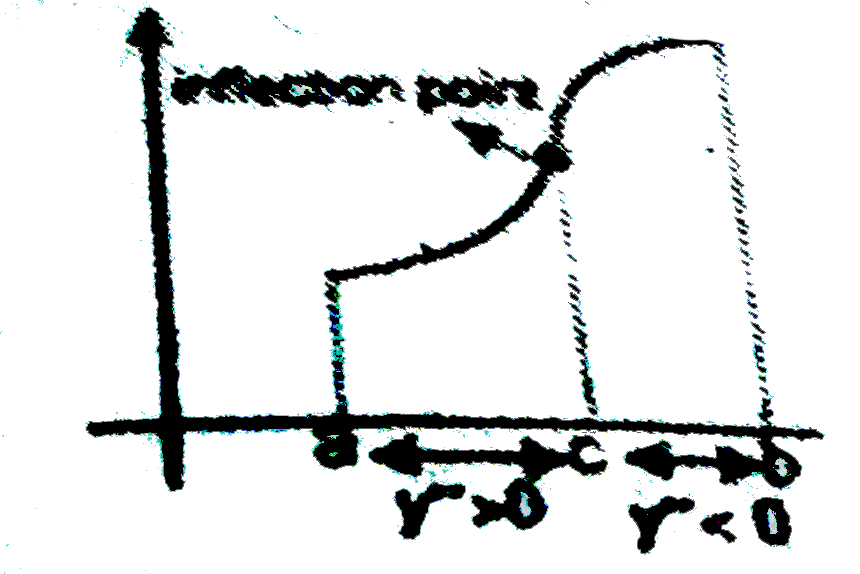
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :A1B2C3D4
Find the inflection points of the curve y=(x−5)5/3+2 .
View Solutionf(x)=x15 at x=0 has inflection point. y D.N.E. at x=0
View SolutionPoint of inflection and point of inflexion
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
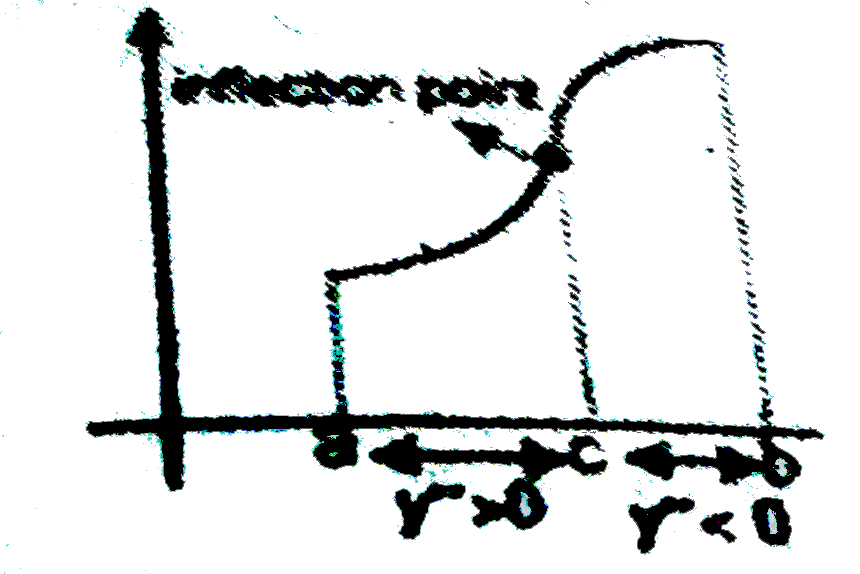
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionThe area bounded by the curve y=xe−x;xy=0and x=c where c is the x-coordinate of the curve's inflection point, is
View Solution
