A projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find
The distance of the target from the hill.
Distance =98×10=980m.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERES
43 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS
60 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View Solution
Knowledge Check
A projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
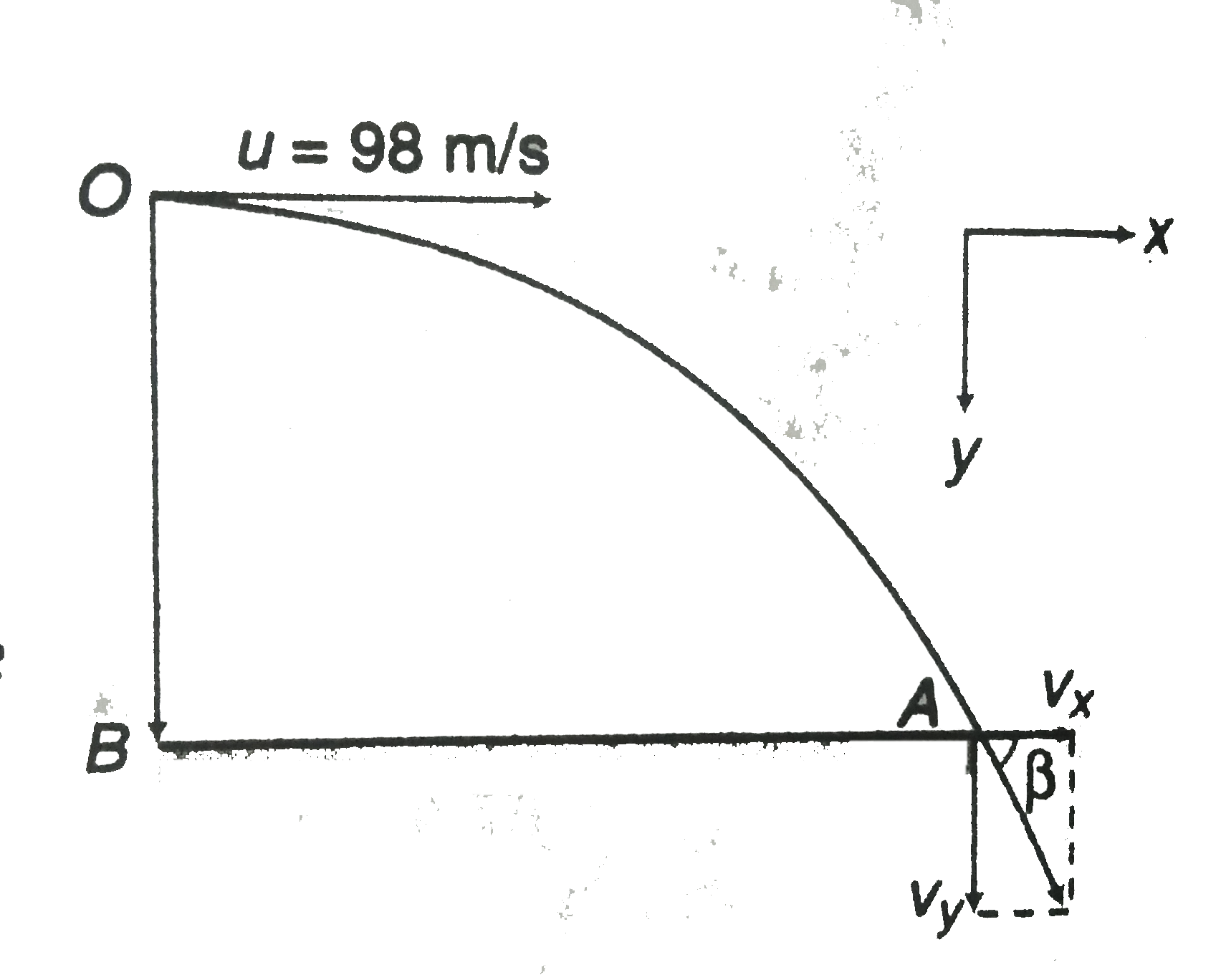 .A12s , 980m , 98(√2)m/s β=45B10s , 98m , 98(√2)m/s β=45C10s , 980m , 98m/s β=45D10s , 980m , 98(√2)m/s β=45
.A12s , 980m , 98(√2)m/s β=45B10s , 98m , 98(√2)m/s β=45C10s , 980m , 98m/s β=45D10s , 980m , 98(√2)m/s β=45a projectile is fired from the surface of the earth with a velocity of 5ms−1 and angle θ with the horizontal. Another projectile fired from another planet with a velocity of 3ms−1 at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth.The value of the acceleration due to gravity on the planet is in ms−2 is given (g=9.8ms−2)
A3.5B5.9C16.3D110.8
A projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
 .
.
View SolutionA particle is fired horizontally with a velocity of 100ms−1 for the top of a hill 400m high. Find (i) the time taken to reach the ground (ii) thedistance of the target from the hill and (iii) the velocity with which the projectile hits the ground. Take g=10ms−2.
View SolutionFrom the top of a hill 480 m high , a projectile is fired horizontally with a speed of 96m/s . Calculate
(i) the time taken by projectile to reach the ground .
(ii) the distance of the target from the hill .
(iii) the velocity with which the projectile hits the ground . Take g=10ms−2
View Solutiona projectile is fired from the surface of the earth with a velocity of 5ms−1 and angle θ with the horizontal. Another projectile fired from another planet with a velocity of 3ms−1 at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth.The value of the acceleration due to gravity on the planet is in ms−2 is given (g=9.8ms−2)
View SolutionA ball is thrown horizontally at a speed v0 from the top of a hill whose slope is a (to the horizontal). Assuming the ball's impact on the hill's surface to be elastic find the point where it will hit the hill the second time.
View Solution
