Question

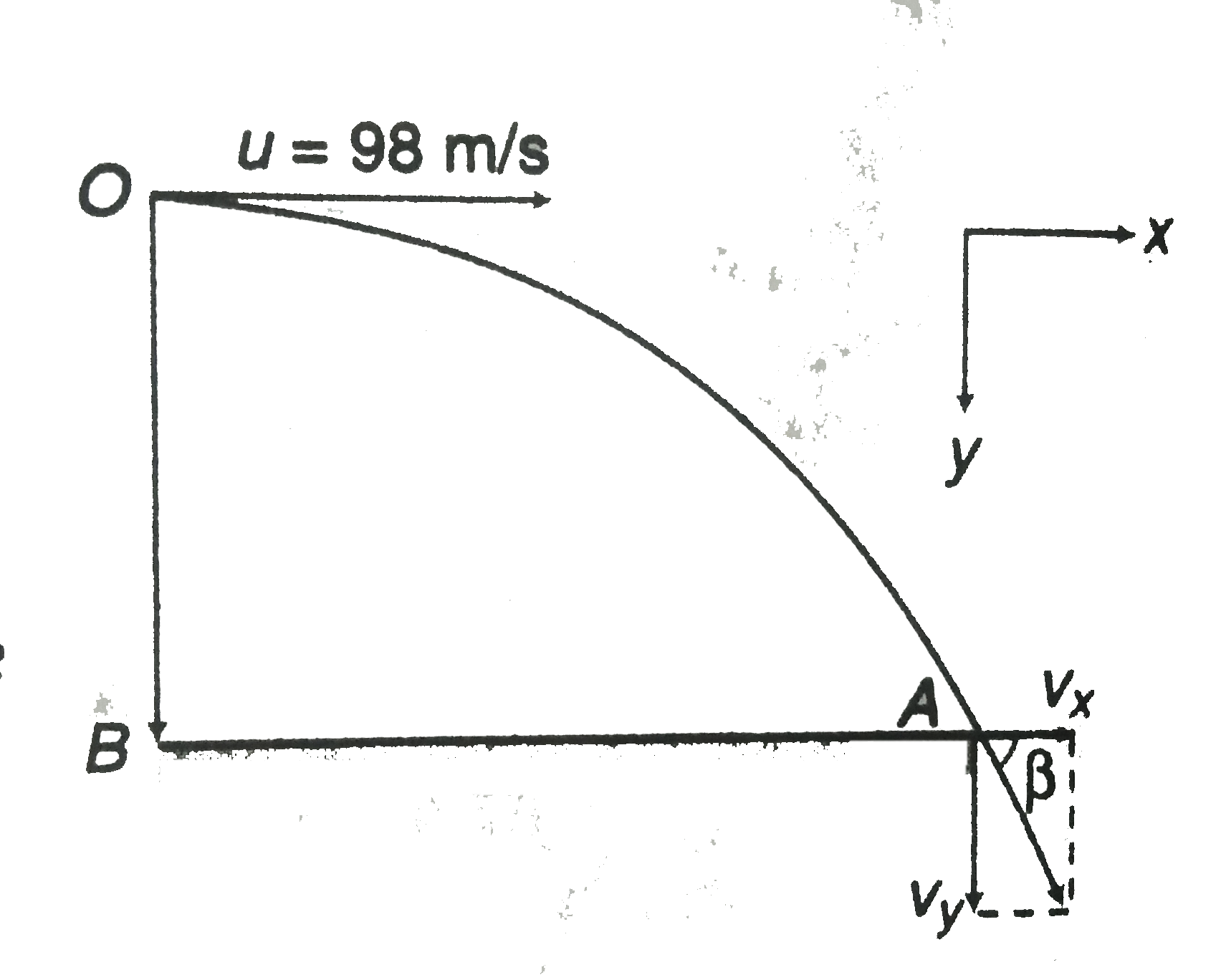
A projectile is fired horizontally with a velocity of $98m{s}^{-1}$ from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.

Explanation

To solve the problem step by step, we will break it down into three parts as requested: (i) time taken to reach the ground, (ii) distance of the target from the hill, and (iii) velocity with which the projectile hits the ground.

Step 1: Calculate the Time Taken to Reach the Ground

1. Identify the known values:
- Height (h) = 490 m
- Initial vertical velocity (u_y) = 0 m/s (since it is fired horizontally)
- Acceleration due to gravity (g) = 9.8 m/s²

2. Use the formula for vertical motion:
The vertical displacement can be described by the equation:
\( h = u_y t + \frac{1}{2} g t^2 \)
Substituting the known values:
\( 490 = 0 \cdot t + \frac{1}{2} \cdot 9.8 \cdot t^2 \)
This simplifies to:
\( 490 = 4.9 t^2 \)

3. Solve for t:
\( t^2 = \frac{490}{4.9} = 100 \)
\( t = \sqrt{100} = 10 \text{ seconds} \)

Step 2: Calculate the Distance of the Target from the Hill

1. Identify the horizontal velocity:
- Initial horizontal velocity (u_x) = 98 m/s

2. Use the time calculated to find the range:
The horizontal distance (range, r) can be calculated using:
\( r = u_x \cdot t \)
Substituting the known values:
\( r = 98 \cdot 10 = 980 \text{ meters} \)

Step 3: Calculate the Velocity with Which the Projectile Hits the Ground

1. Determine the horizontal and vertical components of the final velocity:
- Horizontal component (v_x) = u_x = 98 m/s (remains constant)
- To find the vertical component (v_y), use the following kinematic equation:
\( v_y^2 = u_y^2 + 2g h \)
Substituting the known values:
\( v_y^2 = 0 + 2 \cdot 9.8 \cdot 490 \)
\( v_y^2 = 9604 \)
\( v_y = \sqrt{9604} = 98 \text{ m/s} \)

2. Calculate the resultant velocity (V):
The resultant velocity can be calculated using Pythagoras' theorem:
\( V = \sqrt{v_x^2 + v_y^2} \)
Substituting the values:
\( V = \sqrt{98^2 + 98^2} = \sqrt{9604 + 9604} = \sqrt{19208} = 98\sqrt{2} \text{ m/s} \)

Summary of Results
- (i) Time taken to reach the ground: 10 seconds
- (ii) Distance of the target from the hill: 980 meters
- (iii) Velocity with which the projectile hits the ground: 98√2 m/s