Consider the following figures 1 and 2. In figure 1, the mass of the body A in air is 0.2 kg. The mass of the water container (with water in it) is 0.5 kg. In figure 2, when A is completely immersed in the water of the container B, the readings of the respective balances change as shown.

What is the value of X?
0.55 kg
0.15 kg
0.3 kg
0.45 kg
The correct Answer is:A
Initially, weight of A = 0.2 kg wt
Weight of B = 0.5 kg wt
After complete immersion of A in water,
Weight of A = 0.15 kg wt
Reduction in weight of A = 0.2 - 0.15 = 0.05 kg wt
So, buoyant force applied on A by water = 0.05 kg wt
Required weight = weight of B + buoyant force on A
=0.5+0.05=0.55 kg wt
The reading of X = 0.55 kg
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A container contains 35 kg water and 0.2 kg water leaks from the container. Find the amount of water in container.
A34.8 kgB35 kgC34.80 kgD35.0 kg - Question 2 - Select One
The reading of a spring balance when a mass is weighed on it in air is 40 gm. When the mass is immersed in water, its reading is 20 gm. The specific gravity of the mass is
A3B2C1.5D2.5 - Question 3 - Select One
In the system shown in the figure, the acceleration of 1 kg mass is
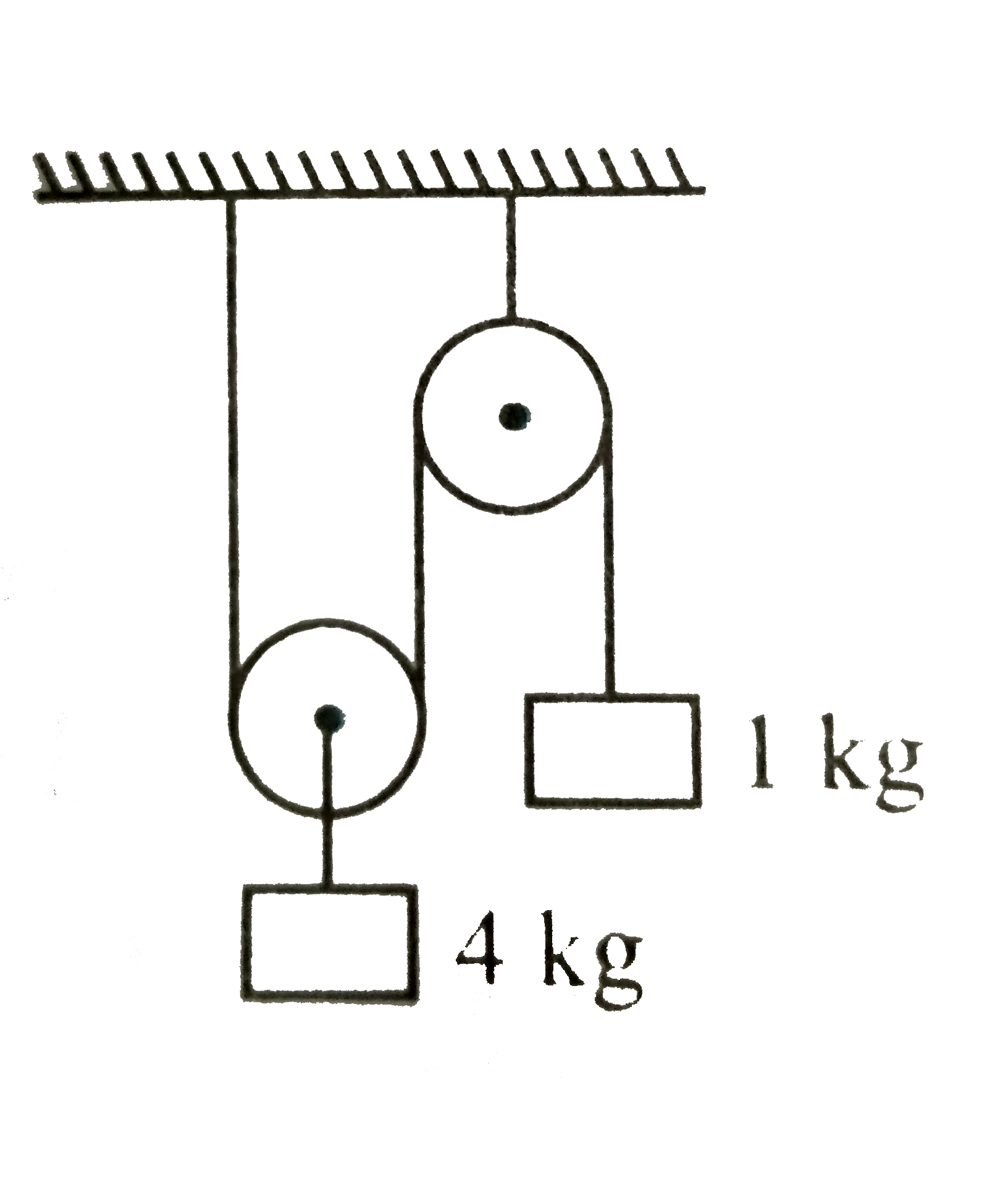 Ag4downwardsBg2downwardsCg2upwardsDg4upwards
Ag4downwardsBg2downwardsCg2upwardsDg4upwards
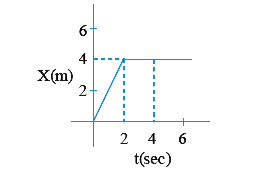
In the figure given, the position-time graph of a particle of mass 0.1 kg is shown the impulse at t = 2s is
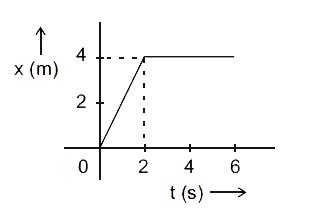 View Solution
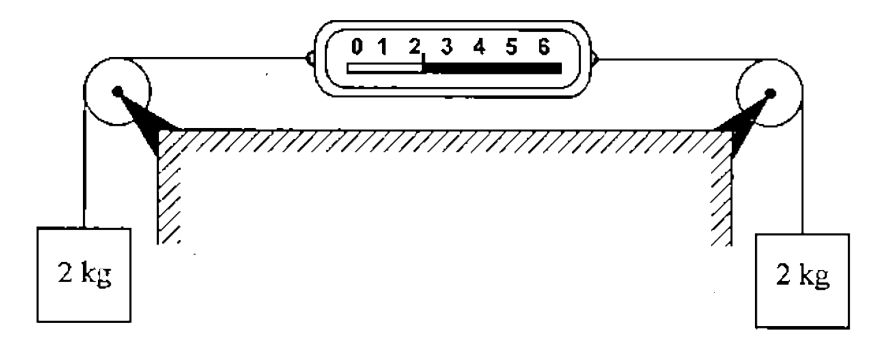
View SolutionAs shown in the figure, two equal masses each of 2kg are suspended from a spring balance. The reading of the spring balance will be.
 View Solution
View SolutionIn the figure given below, the position time graph of a particle of mass 0.1kg is shown. The impulse at t=2 sec is
 View Solution
View SolutionA metallic sphere of mass 2 . 0 kg and volume 2.5×10−4m3 is completely immersed in water. Find the buoyant force exerted by water on the sphere
Density of water =1000kg/m3View SolutionA block of aluminium of mass 1kg and volume 3.6×10−4m3 is suspended from a string and then completely immersed in a container of water. The decrease in tension in the string after immersion is.
View Solution