A tank 2 m high is half filled with water and then filled to the top with oil of density 0.60 g/cc. What is the pressure at the bottom of the tank due to these liquids? (Take g = 10 m s−2)
0.8×102Nm−2
0.8×104Nm−2
1.6×102Nm−2
1.6×104Nm−2
The correct Answer is:D
Density of oil (ρo) = 0.60 g/cc = 600 kg/m3
Density of water (ρw)=1g/cm3=1000kg/m3
Pressure due to water =hρwg
=1×1000×10=10000Nm−2
Pressure due to oil =hρog
=1×600×10=6000Nm−2
Total pressure =10000+6000
=16000Nm−2=1.6×104Nm−2
Topper's Solved these Questions
Similar Questions
A water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View SolutionIf pressure at the half depth of a lake is equal to 34 times the pressure at its bottom, then find the depth of the lake. [Take g = 10 m/s2]
View Solution
Knowledge Check
- Question 1 - Select One
A tank 5 m high is half filled with water and then is filled to the top with oil of density 0.85 g The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2 - Question 2 - Select One
A tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2 - Question 3 - Select One
A uniformly tapering vessel is filled with a liquid of density 900kg/m. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)(upper area=10−3m2,lower area=2×10−3m2)
 A3.6NB7.2NC9.0ND14.4N
A3.6NB7.2NC9.0ND14.4N
A rectangular tank is 10m long 5m broad and 3m high. It is filled to the rim with water of density 103kgm−3. Calculate the thrust at the bottom and walls of the tank due to hydrostatic pressure. Take g=9.8ms−2.
View SolutionA cylinder of 4 m height is half filled with oil of density 0.72 g cm−3. If the Becond half of cylinder is filled with water, then find the pressure at the bottom of cylinder due to these liquids.
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
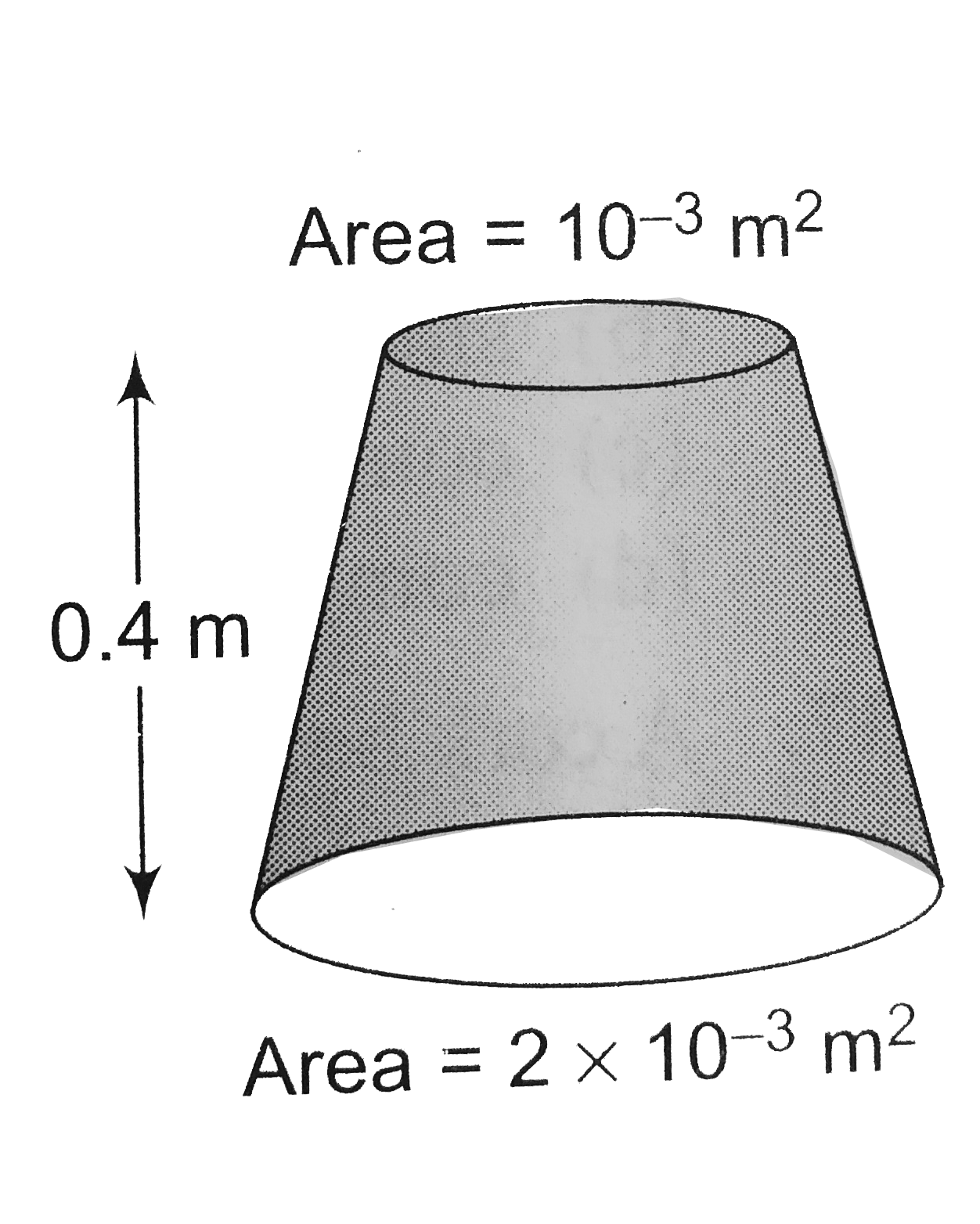 View Solution
View SolutionA hole is made at the bottom of the tank filled with water (density =1000kgm−3). If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere =105Nm−2), then the velocity of efflux is nearest to
View SolutionA tank is filled with water of density 1gcm−3 and oil of density 0.9gcm−3 . The height of the water layer is 100 cm and of the oil layer is 400 cm. If g = 980 cms−2 , then the velocity of efflux from an opening in the bottom of the tank is
View Solution
