A biconvex lens has radii of curvature 20 cm and 15 cm each. The refractive index of the material of the lens is 1.5. What is its focal length? Will the focal length change if the lens is flipped by the side?
For a biconvex lens, radius of curvature of the first surface is positive and that of the second surface is negative side as shown in the figure
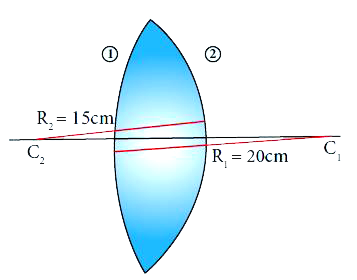
Given, n=1.5,R1=20 cm and R2=−15 cm
Lens maker’s formula, 1f=(n−1)(1R1−1R2)
Substituting the values,
1f=(1.5−1)(120−1−15)
1f=(0.5)(120+115)=(0.5)(3+460)=(12×760)=7120
f=1207=17.14 cm
As the focal length is positive the lens is a converging lens.
If the lens is flipped back to front,

Now, R1=15 cm and R2=−20 cm, n=1.5
Substituting the values, 1f=(1.5−1)(115−1−20)
1f=(1.5−1)(115+120)
This will also result in, f=17.14 cm
Thus, it is concluded that the focal length of the lens will not change if it is flipped side wise. This is true for any lens. Students can verify this for any lens.
Topper's Solved these Questions
- OPTICSBook:NCERT TAMILChapter:OPTICSExercise:EVALUATION (Multiple choice questions)
Explore 20 Videos
- OPTICSBook:NCERT TAMILChapter:OPTICSExercise:EVALUATION (Numerical Problems)
Explore 10 Videos
- NUCLEIBook:NCERT TAMILChapter:NUCLEIExercise:ADDITIONAL EXERCISES
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT TAMILChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:EXERCISES
Explore 40 Videos
Similar Questions
Knowledge Check
A double convex lens has faces of radii of curvature 30 cm each. The refractive index of the material of the lens is 1.5. What is the focal length of this lens when immersed is carbondisulphide of refractive index 1.6 ?
A−120cmB−180cmC−200cmD−240cmThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
A24 cmB10 cmC20 cmD24cmThe radii of curvature of the two surface of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5 . If the lens is concave - convex, then the focal length of the lens is :
A24 cmB10 cmC15 cmD120 cm
A biconvex lens has radii of curvature 20 cm and 40cm. The refractive index of the material of the lens is 1.5. An object is placed 40cm in front of the lens. Calculate the psition of the image.
View SolutionA biconvex lens has radii of curvature 20 cm and 40cm. The refractive index of the material of the lens is 1.5. An object is placed 40cm in front of the lens. Calculate the psition of the image.
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View Solution
