A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

ML
2ML
4 ML
16 ML
The correct Answer is:D
f=2π:ω=2πf=4rad/sec
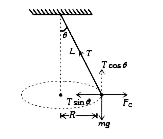
Tsinθ=Mω2R
R=Lsinθ
⇒Tsinθ=Mω2Lsinθ
⇒T=16ML
Similar Questions
A string of length 1 m is fixed at one end to a rigid support and carries a sphere of 100 g at the other end. The string makes 2π revolutions per second around a vertical axis through the fixed end. Calculate
The angle of inclination of the string with the vertical axis.
View SolutionA string of length 1 m is fixed at one end to a rigid support and carries a sphere of 100 g at the other end. The string makes 2π revolutions per second around a vertical axis through the fixed end. Calculate
The tension in the string and.
View SolutionA string of length L is fixed at one end and carries a mass M at the other end . The string makes 2/π revlutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is
View SolutionA string of length L fixed at one end carries a mass M at the other end. The string makes 2π revolutions per second around the vertical axis through the fixed end as shown in the figure what is the tension in the string ?
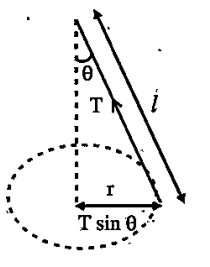
View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
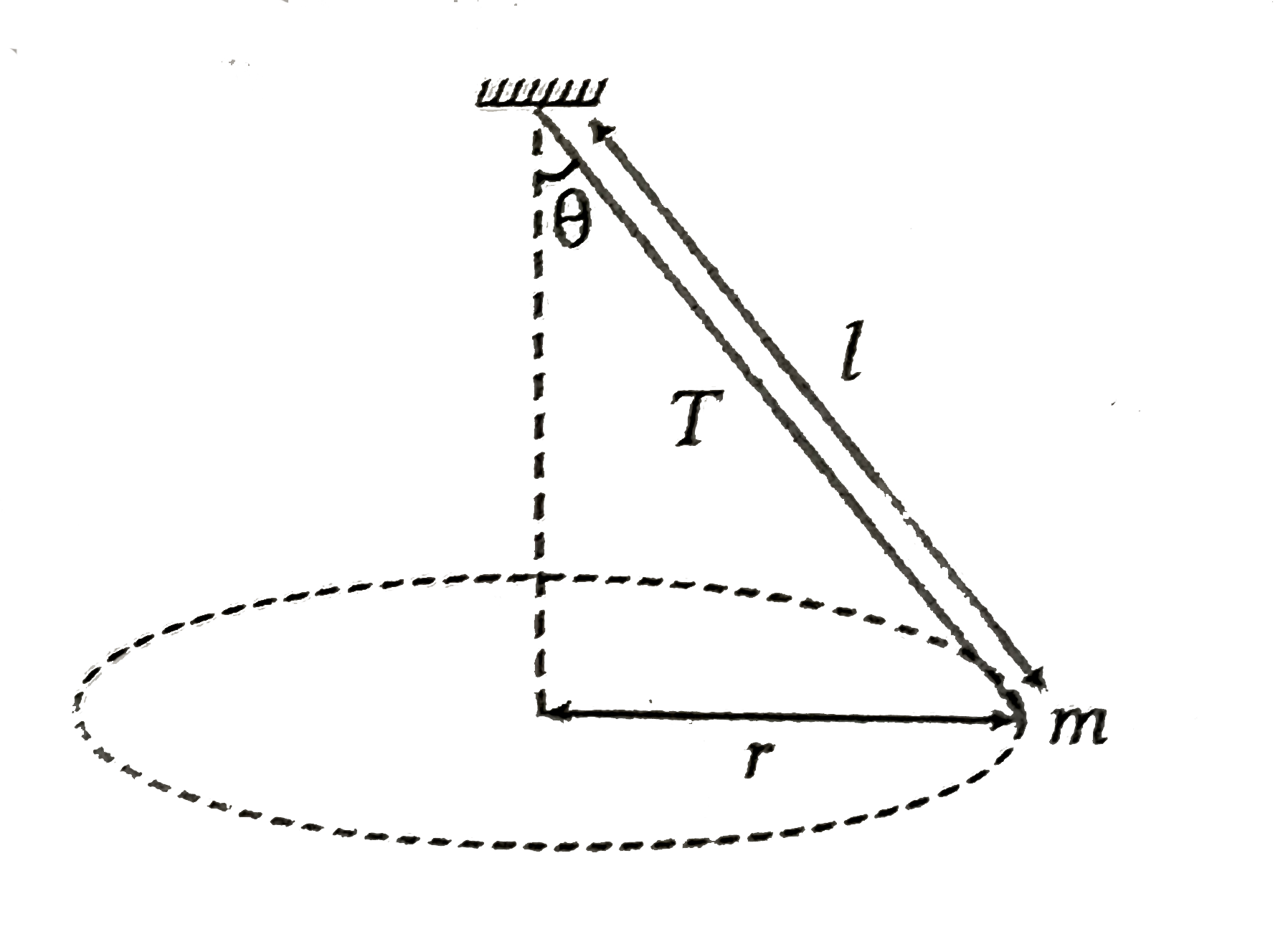
View SolutionA string of length L is fixed at one end and the string makes 2π rev/s around the vertical axis through the fixed end as shwon in thefigure, then tension in the string is
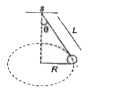
View SolutionOne end of a string of length 1 m is fixed with a sphere of mass 100 g and the string is rotated about a vertical axis through a fixed point. 2/pi revolutions per second. The angle of inclination of the string with the vertical is:
View SolutionA string of length is fixed at one end and carries a mass M at the other end. The string makes .2πp.s. about a vertical axis through the fixed end. The angle which the string subtends with vertical is:
View Solution