Two blocks (1 and 2) of equal mass m are connected by an ideal string (see figure shown) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants k1 and k2 such that k1>k2
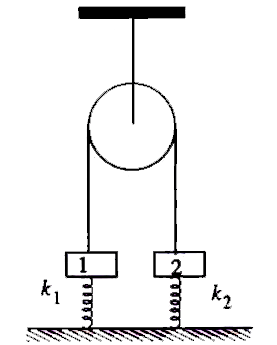
Initially, both springs are unstretched. The block 1 is slowly pulled down a distance x and released. Just after the release the possible values of the magnitude of the acceleration of the blocks a1 and a2 can be–
Either (a1=a2=(k1+k2)2m)or(a1=k1Xm−g) and (a2=k3xm+g)
(a1=a2=(K1+k2)x2m) Only
(a1=a2=(k1−k2)x2m)Only
Either (a1=a2(K1−k2)2m)or(a1=a2(k1k2)(k1+k2)m−g)
The correct Answer is:B
When block 1 is slowly pulled down as distance x and released
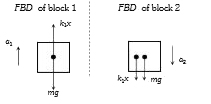
k1x−mg=ma1 …….(i)
⇒a1=k1xm−g
k2x+mg=ma2 ………..(ii)
if a1=a2, then add equation (i) + (ii)
2ma=k1x+k2x
⇒a=a1=a2=(k1+k2)x2m
Similar Questions
A block of mass M is placed on a smooth table. Its two sides are attached to fixed walls by means of collinear horizontal springs of spring constants k_(1) and k_(2)(k_(1)gt k_(2)) as shown in the Figure. The block is made to oscillate horizontally along the line of the two springs. The frequency of its oscillation is :
View SolutionA block of mass m be placed on a frictionless surface of a table. Spring constants of a spring joint on both side are k_(1)" and "k_(2) if block. Leave the block by slight displaced it, then its angular frequency will be……….
View SolutionA block of m mass, as shown, spring constant k_(1)" तथा "k_(2) Vali is connected to two springs. | The block is left by displacing to the right by x distance. When the block is at x / 2 distance, the velocity of the block will be: (A) sqrt(((k_(1)+k_(2))x^(2))/(2m)) (B) sqrt((3(k_(1)+k_(2))x^(2))/(4m)) (C ) sqrt(((k_(1)+k_(2))x^(2))/(m)) (D) sqrt(((k_(1)+k_(2))x^(2))/(4m))
View SolutionA 2kg block is connected with two springs of force constants K1=100 N/m and K2=300 N/m as shown in figure. The block is released from rest with the springs unstretched. Find the acceleration of the block in its lowest position (g=10m/s2)

View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

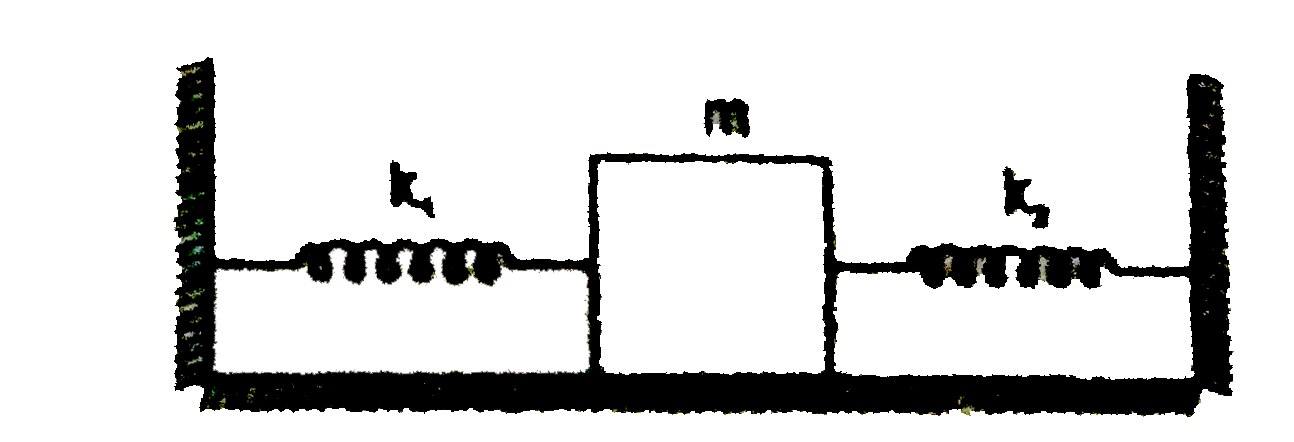
View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
View SolutionA 2 kg block is connected with two springs of force constants k_(1)=100 N//m and k_(2)=300 N//m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10 m//s^(2))
View SolutionAs shown in the figure, two light springs of force constant k_(1) and k_(2) oscillate a block of mass m. Its effective force constant will be
View Solution
