In the given figure we have ∠1=∠2,∠3=∠4. Then
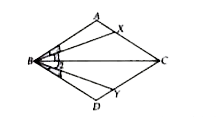
∠ABC=∠DBC
∠ABC≠∠DBC
∠BAX=∠BXC
None of these
The correct Answer is:A
Topper's Solved these Questions
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL -2 MATCH THE FOLLOWING)
3 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL -2 ASSERTION AND REASON TYPE)
2 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL -1)
15 Videos
- HERON'S FORMULABOOK - MTG IIT JEE FOUNDATIONCHAPTER - HERON'S FORMULAEXERCISE - OLYMPIAD/HOTS CORNER
7 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - OLYMPIAD/HOTS CORNER
5 Videos
Similar Questions
In the given figure (1) If ∠1=∠2 and ∠2=∠3 then prove that ∠1=∠3 (2) If ∠1=∠3 and ∠2=∠4 then prove ∠A=∠C (3) If ∠1=∠3, ∠2=∠4 and ∠3=∠4 write the relation between ∠1 and ∠2 using Euclids axiom
View SolutionIn the given figure if ∠1=30∘ find ∠2&∠3
View SolutionIn the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
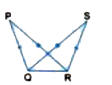
View SolutionIn the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
View SolutionIn the given figure we have AO=BO and CO=DO. Prove that :
(i) ΔAOC≅ΔBOD
AC=BD

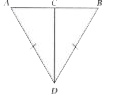
View SolutionIn the given figure, we have C is the mid-point of AB and DA = DB.
Prove that : ∠DCA=∠DCB.
View SolutionIn the given figure we have ∠1=∠3,∠2=∠4and∠3=∠4 prove that ∠1=∠2
View SolutionIn the given figure, we have AO = BO and CO = DO. Prove that ΔAOC≅ΔBOD.

View SolutionIn the given figure, we have PQ = SR and Pr = SQ. Prove that:

∠PQR=∠SRQ
View SolutionIn the given figure, we have PQ = SR and Pr = SQ. Prove that:
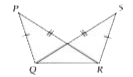
ΔPQR≅ΔSRQ
View Solution
