Assertion : If TP and TQ are the two tangents to a circle with centre O so that ∠POQ=123∘, then ∠PTQ=57∘.
Reason : OPTQ is a cyclic quadrilateral.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true and reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is true.
The correct Answer is:A
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Comprehension (Passage-I))
4 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Comprehension (Passage-Ii))
4 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Match the following)
6 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
Knowledge Check
TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘If TP and TQ are two tangents to a circle with centre O, so that ∠POQ=120∘, then ∠PTQ is equal to
A120∘B30∘C60∘D90∘If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
A90∘B45∘C30∘D60∘
In the given figure , if TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘ , then ∠PTQ is equal to
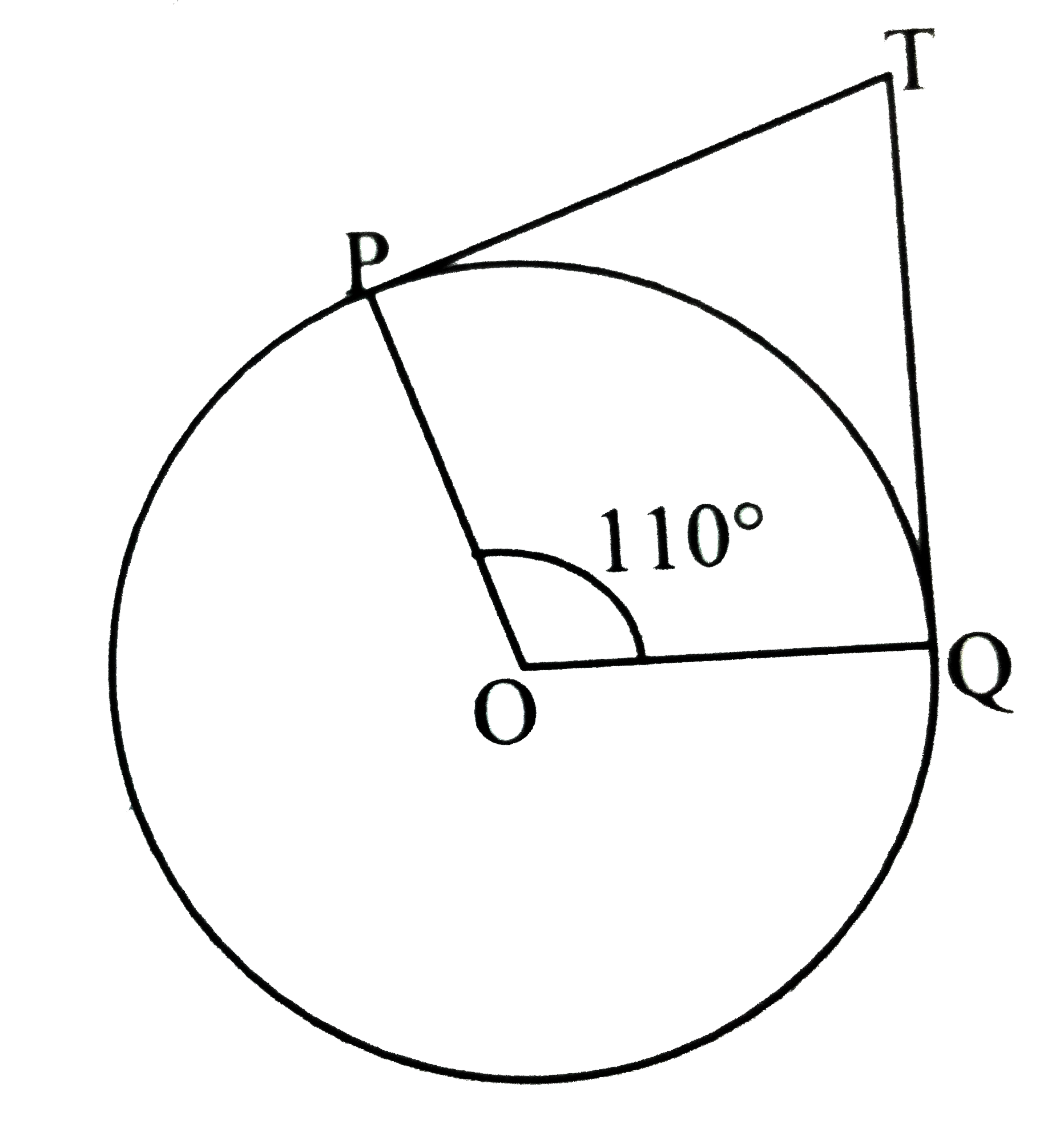
View SolutionIf TP and TQ are the two tangents to a circle with centre O. So that ∠PQR=105∘, then ∠PTQ is ………….. .
View SolutionIn the given figure ,if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘ ,then ∠PTQ is

View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionIn the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘, then ∠PTQ is
View Solution
